��Ŀ����
����Ŀ��ij��ѧ�ڿ�ѧ��������һ�ֺз������Դ�ҵ����һ����ѧ���ڣ�ÿ�۳�1�иúз�������10Ԫ��δ�۳��IJ�Ʒ��ÿ�п���5Ԫ��������ʷ���ϣ��õ���ѧ���г���������Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ����ͬѧΪ�����ѧ��������150�иò�Ʒ����![]() ����λ���У�
����λ���У�![]() ����ʾ�����ѧ���ڵ��г���������
����ʾ�����ѧ���ڵ��г���������![]() ����λ��Ԫ����ʾ�����ѧ���ھ����ò�Ʒ������
����λ��Ԫ����ʾ�����ѧ���ھ����ò�Ʒ������
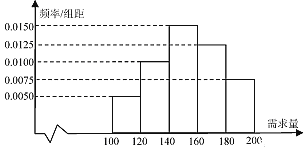
������ֱ��ͼ���������ѧ�����г�������![]() ��ƽ������������
��ƽ������������
����![]() ��ʾΪ
��ʾΪ![]() �ĺ�����
�����
������Ƶ�ʷֲ�ֱ��ͼ��������![]() ������1350Ԫ�ĸ��ʣ�
������1350Ԫ�ĸ��ʣ�
���𰸡�����ƽ����Ϊ153������Ϊ150; ����![]() ��
��![]() ; ����0.7.
; ����0.7.
�����������������
(1)���Ƶ�ʷֲ�ֱ��ͼ�ɵ�ƽ����![]() ���Ķ�ֱ��ͼ�ɵ�����Ϊ150.
���Ķ�ֱ��ͼ�ɵ�����Ϊ150.
(2)������ɽ�����д�ɷֶκ�������ʽ�� ![]() ��
�� ![]() ;
;
(3)���������г�����ʽ�����(1)�Ľ��ۿɵ�����![]() ������1350Ԫ�ĸ���Ϊ0.7.
������1350Ԫ�ĸ���Ϊ0.7.
���������
������Ƶ�ʷֲ�ֱ��ͼ�ã����������Ϊ150�е�Ƶ��Ϊ![]() .
.
�����ѧ�����г�����������������ֵ��150.
������Ϊ[100,120����Ƶ��Ϊ![]() ��
��
������Ϊ[120,140����Ƶ��Ϊ![]() ��
��
������Ϊ[140,160����Ƶ��Ϊ![]() ��
��
������Ϊ[160,180����Ƶ��Ϊ![]() ��
��
������Ϊ[180,200����Ƶ��Ϊ![]() ��
��
��ƽ����
![]()
![]() .
.
�Ķ�ֱ��ͼ�ɵ�����Ϊ150.
������Ϊÿ�۳�1�иúз�������10Ԫ��δ�۳��ĺз���ÿ�п���5Ԫ��
���Ե�![]() ʱ��
ʱ��![]()
![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
����![]() ��
��![]() .
.
������Ϊ��������1350Ԫ������![]() �����
�����![]() .
.
�����ɣ���֪��������1350Ԫ�ĸ���![]() .
.

 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д�