Question

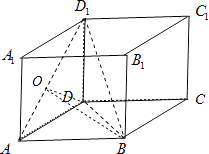
【题目】如图，已知直四棱柱ABCD﹣A1B1C1D1 ， DD1⊥底面ABCD，底面ABCD为平行四边形，∠DAB=45°，且AD，AB，AA1三条棱的长组成公比为 的等比数列，

（1）求异面直线AD1与BD所成角的大小；
（2）求二面角B﹣AD1﹣D的大小．

Answer 1

【答案】
（1）解：不妨设AD=1，∵AD，AB，AA1三条棱的长组成公比为 的等比数列，∴AB= ，AA1=2．

在△ABD中，DB2= =1，解得DB=1．∴AD2+DB2=AB2，∠ADB=90°．

∴AD⊥DB．

∵DD1⊥底面ABCD，DB平面ABCD，∴DD1⊥DB，

又AD∩DD1=D，

∴DB⊥平面ADD1，

∴DB⊥AD1，

∴异面直线AD1与BD所成角为90°

（2）解：由（1）可得：DB⊥平面ADD1．

在Rt△ADD1中，经过点D作DO⊥AD1，垂足为O，连接OB，则OB⊥AD1．

∴∠BOD即为二面角B﹣AD1﹣D的平面角．

在Rt△ADD1中，OD= = = ．

在Rt△ODB中，tan∠BOD= = = ．

∴∠BOD=arctan ．

【解析】（1）不妨设AD=1，由AD，AB，AA1三条棱的长组成公比为 的等比数列，可得AB= ，AA1=2．在△ABD中，利用余弦定理可得：DB=1．利用勾股定理的逆定理可得∠ADB=90°．由DD1⊥底面ABCD，可得DD1⊥DB，可得DB⊥平面ADD1 ， 即可得出异面直线AD1与BD所成角．（2）由（1）可得：DB⊥平面ADD1 ． 在Rt△ADD1中，经过点D作DO⊥AD1 ， 垂足为O，连接OB，可得OB⊥AD1 ． ∠BOD即为二面角B﹣AD1﹣D的平面角．利用直角三角形的边角关系即可得出．
【考点精析】解答此题的关键在于理解异面直线及其所成的角的相关知识，掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系．