题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)若存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)单调递减区间为![]() ,
,![]() ;单调递增区间为
;单调递增区间为![]() ,
,![]() .(2)
.(2)![]()
【解析】
(1)根据题意,代入![]() ,求导,利用导数的正负求解单调区间
,求导,利用导数的正负求解单调区间
(2)根据题意,对函数求导,因为存在![]() ,使得
,使得![]() 成立,所以
成立,所以![]() 在区间
在区间![]() 上存在极值点,转化成
上存在极值点,转化成![]() 在区间
在区间![]() 上有解,再转化成
上有解,再转化成![]()
![]() 有解,令
有解,令![]()
![]() ,根据导数求解
,根据导数求解![]() 的值域,即可求解参数取值范围.
的值域,即可求解参数取值范围.
(1)由![]() ,
,
得![]()
![]() .
.
令![]() ,则
,则![]()
![]() ,
,
解得![]() ,
,![]() ,
,![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
综上,函数![]() 的单调递减区间为
的单调递减区间为![]() ,
,![]() ;
;
单调递增区间为![]() ,
,![]() .
.
(2)由已知可得![]()
![]() .
.
因为存在![]() ,使得
,使得![]() 成立,
成立,
所以![]() 在区间
在区间![]() 上存在极值点,所以
上存在极值点,所以![]() 在区间
在区间![]() 上有解.
上有解.
所以![]() ,即
,即![]()
![]() 有解.
有解.
令![]()
![]() ,则
,则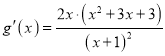 ,
,
当![]() 时,
时,![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() .
.
又![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() .
.
即实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目
【题目】某面包店推出一款新面包,每个面包的成本价为4元,售价为10元,该款面包当天只出一炉(一炉至少15个,至多30个),当天如果没有售完,剩余的面包以每个2元的价格处理掉.为了确定这一炉面包的个数,该店记录了这款新面包最近30天的日需求量(单位:个),整理得下表:
日需求量 | 15 | 18 | 21 | 24 | 27 |
频数 | 10 | 8 | 7 | 3 | 2 |
(1)根据表中数据可知,频数![]() 与日需求量
与日需求量![]() (单位:个)线性相关,求
(单位:个)线性相关,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)以30天记录的各日需求量的频率代替各日需求量的概率,若该店这款新面包出炉的个数为24,记当日这款新面包获得的总利润为![]() (单位:元).
(单位:元).
(i)若日需求量为15个,求![]() ;
;
(ii)求![]() 的分布列及其数学期望.
的分布列及其数学期望.