题目内容
若函数y=log2(kx2+4kx+3)的定义域为R,则k的取值范围是( )
A.(0,
| B.[0,
| C.[0,
| D.(-∞,0]∪(
|
要使函数y=log2(kx2+4kx+3)的定义域为R,则kx2+4kx+3>0恒成立.
若k=0,则不等式kx2+4kx+3>0等价为3>0,∴k=0成立.
若k≠0,要使为kx2+4kx+3>0恒成立,则
,
即
,解得0<k<
.
综上:0≤k<
.
故选C.
若k=0,则不等式kx2+4kx+3>0等价为3>0,∴k=0成立.
若k≠0,要使为kx2+4kx+3>0恒成立,则
|
即
|
| 3 |
| 4 |
综上:0≤k<
| 3 |
| 4 |
故选C.

练习册系列答案
相关题目

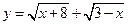 (2)
(2)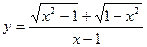
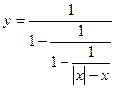
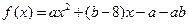 ,当
,当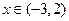 时,
时,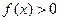 ;当
;当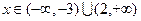 时,
时, .(1)
.(1) 为何值时
为何值时 的解集为
的解集为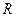 ;(2)求
;(2)求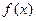 在
在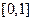 内的值域.
内的值域.
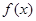 在(0,+∞)上是增函数,又
在(0,+∞)上是增函数,又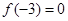 ,则
,则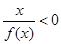 的解集为( ).
的解集为( ).