题目内容
(本题12分)已知函数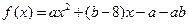 ,当
,当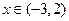 时,
时,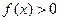 ;当
;当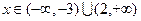 时,
时, .(1)
.(1) 为何值时
为何值时 的解集为
的解集为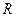 ;(2)求
;(2)求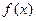 在
在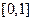 内的值域.
内的值域.
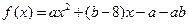 ,当
,当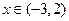 时,
时,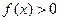 ;当
;当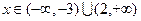 时,
时, .(1)
.(1) 为何值时
为何值时 的解集为
的解集为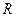 ;(2)求
;(2)求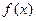 在
在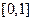 内的值域.
内的值域.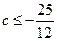 ,
,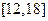
解:由题意可知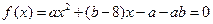 的两根分别为
的两根分别为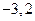 ,且
,且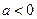 ,则由韦达定理可得:
,则由韦达定理可得: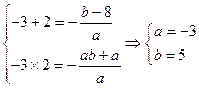 .(1)
.(1)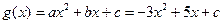 ,则要使
,则要使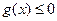 的解集为R,只需要方程
的解集为R,只需要方程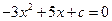 的判别式
的判别式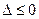 ,即
,即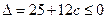 ,解得
,解得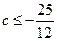 .∴当
.∴当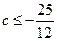 时,
时, 的解集为
的解集为 .
.
(2)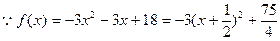 ,
,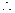
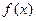 在
在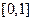 内单调递减,故
内单调递减,故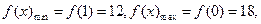 故
故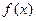 在
在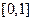 内的值域为
内的值域为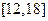 .
.
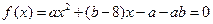 的两根分别为
的两根分别为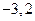 ,且
,且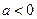 ,则由韦达定理可得:
,则由韦达定理可得: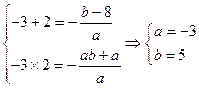 .(1)
.(1)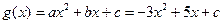 ,则要使
,则要使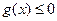 的解集为R,只需要方程
的解集为R,只需要方程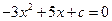 的判别式
的判别式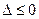 ,即
,即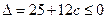 ,解得
,解得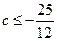 .∴当
.∴当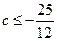 时,
时, 的解集为
的解集为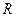 .
.(2)
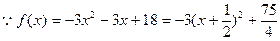 ,
,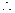
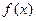 在
在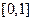 内单调递减,故
内单调递减,故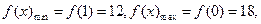 故
故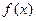 在
在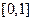 内的值域为
内的值域为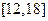 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
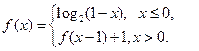 则
则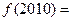 ( )
( )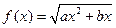 ,存在一个正数
,存在一个正数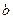 ,使得
,使得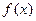 的定义域和值域相同,则非零实数
的定义域和值域相同,则非零实数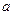 的值为__________.
的值为__________.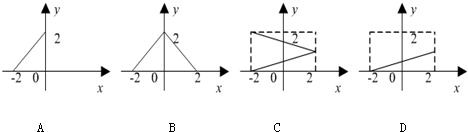
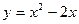 的定义域为
的定义域为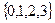 ,那么其值域为 ( )
,那么其值域为 ( )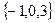
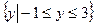
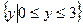
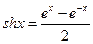 ,双曲余弦函数:
,双曲余弦函数: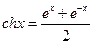 ,则函数
,则函数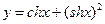 的值域为 .
的值域为 .