题目内容
9.已知△ABC是锐角三角形,P=sinA+sinB,Q=cosA+cosB,则P与Q的大小关系为P>Q.分析 作差由和差化积公式可得P-Q=2cos$\frac{A-B}{2}$(sin$\frac{A+B}{2}$-cos$\frac{A+B}{2}$),由锐角三角形角的范围可判每个式子的正负,由此可得结论.
解答 解:由题意可得P-Q=(sinA+sinB)-(cosA+cosB)
=2sin$\frac{A+B}{2}$cos$\frac{A-B}{2}$-2cos$\frac{A+B}{2}$cos$\frac{A-B}{2}$
=2cos$\frac{A-B}{2}$(sin$\frac{A+B}{2}$-cos$\frac{A+B}{2}$)
∵△ABC是锐角三角形,∴A+B=π-C>$\frac{π}{2}$,
∴$\frac{A+B}{2}$>$\frac{π}{4}$,∴sin$\frac{A+B}{2}$>cos$\frac{A-B}{2}$,
由A和B为锐角可得-$\frac{π}{4}$<$\frac{A-B}{2}$<$\frac{π}{4}$,∴cos$\frac{A-B}{2}$>0,
∴P-Q>0,即P>Q,
故答案为:P>Q.
点评 本题考查两角和与差的三角函数公式,涉及和差化积公式及三角函数的值域,属中档题.

练习册系列答案
相关题目
4.R是△ABC三角形的外接圆半径,若ab<4R2cosAcosB,则∠C为( )
| A. | 锐角 | B. | 直角 | C. | 钝角 | D. | 无法判断 |
1.斜率为2的直线L经过抛物线y2=2px(p>0)的焦点F,且交抛物线与A、B两点,若AB的中点到抛物线准线的距离1,则P的值为( )
| A. | 1 | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
18.已知函数f(x)=lnx+x2-bx在其定义域内是增函数,则b的取值范围是( )
| A. | (-∞,2$\sqrt{2}$) | B. | (2$\sqrt{2}$,+∞) | C. | (-∞,2) | D. | (2,+∞) |
19.如图,在正方体ABCD-A1B1C1D1中,直线A1B与直线C1D1所成的角为( )
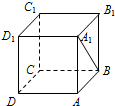

| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
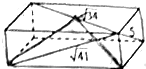 如图,已知长方体过一个顶点的三条面对角线的长分别为5,$\sqrt{34}$,$\sqrt{41}$,则其外接球(长方体的顶点均在球面上)的表面积是50π.
如图,已知长方体过一个顶点的三条面对角线的长分别为5,$\sqrt{34}$,$\sqrt{41}$,则其外接球(长方体的顶点均在球面上)的表面积是50π.