题目内容
4.在△ABC中,根据下列条件,求三角形的面积S(精确到0.01cm2).(1)已知a=28cm,c=33cm,B=45°;
(2)已知A=32.8°,C=66.5°,a=36cm;
(3)已知a=54cm,b=61cm,c=71cm.
分析 (1)利用$S=\frac{1}{2}acsinB$即可得出.
(2)S=$\frac{1}{2}bcsinA$=$\frac{1}{2}×\frac{{a}^{2}sinBsinC}{sinA}$,即可得出;
(3)p=$\frac{1}{2}(a+b+c)$,利用海伦公式可得S=$\sqrt{p(p-a)(p-b)(p-c)}$.
解答 解:(1)$S=\frac{1}{2}acsinB$=$\frac{1}{2}×28×33×\frac{\sqrt{2}}{2}$≈326.63.
(2)由正弦定理可得:$b=\frac{asinB}{sinA}$,$c=\frac{asinC}{sinA}$,
∴S=$\frac{1}{2}bcsinA$=$\frac{1}{2}×\frac{asinB}{sinA}×\frac{asinC}{sinA}×sinA$=$\frac{1}{2}×\frac{{a}^{2}sinBsinC}{sinA}$=$\frac{1}{2}×\frac{3{6}^{2}×sin80.{7}^{°}×sin66.{5}^{°}}{sin32.{8}^{°}}$=$\frac{1}{2}×\frac{1296×0.9869×0.9170}{0.5417}$=1082.58.
(3)p=$\frac{1}{2}(a+b+c)$=93.
∴S=$\sqrt{p(p-a)(p-b)(p-c)}$=$\sqrt{93×39×32×22}$=24$\sqrt{4433}$≈24×66.58≈1597.92.
点评 本题考查了三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
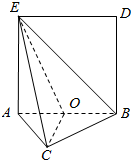 如图,矩形ABDE所在平面与正三角形ABC所在平面互相垂直,AE=3,AB=2$\sqrt{3}$,点O是边AB的中点.
如图,矩形ABDE所在平面与正三角形ABC所在平面互相垂直,AE=3,AB=2$\sqrt{3}$,点O是边AB的中点.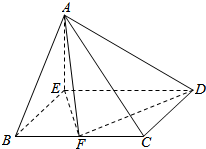 如图所示,在四棱锥A-BCDE中,AE⊥面EBCD且四边形EBCD是菱形,∠BED=120°,AE=BE=2,F是BC上的动点.
如图所示,在四棱锥A-BCDE中,AE⊥面EBCD且四边形EBCD是菱形,∠BED=120°,AE=BE=2,F是BC上的动点.