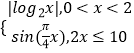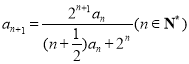题目内容
【题目】已知双曲线
(a>0，b>0)的右准线l2与一条渐近线l交于点P，F是双曲线的右焦点．
(1)求证：PF⊥l；
(2)若PF＝3，且双曲线的离心率e＝
，求该双曲线的方程．
【答案】(1)见解析(2) 
【解析】试题分析：（1）右准线l2为x=
，设渐近线l为y=
x，则kPF＝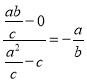
， 
由此能证明PF⊥l．（2）由已知得
，又e＝
，即
解得
由此能求出双曲线方程．
试题解析：
(1)证明：右准线为l2：x＝
，由对称性不妨设渐近线l为y＝
x，则P
，
又F(c,0)，∴kPF＝
＝－
.
又∵kl＝，∴kPF·kl＝－·＝－1.∴PF⊥l.
(2)∵PF的长即F(c,0)到l：bx－ay＝0的距离，
∴
，∴b＝3.又e＝
＝
，
∴
＝
.∴a＝4.
故双曲线方程为
－
＝1.
练习册系列答案
口算题天天练系列答案
相关题目
