题目内容
如图,在棱长是1的正方体ABCD-A1B1C1D1中,点E,F,G分别是DD1,BD,BB1的中点.

(1)求证:EF⊥CF;
(2)求EF与CG所成的角的余弦值;
(3)求三棱锥G-CEF的体积.

(1)求证:EF⊥CF;
(2)求EF与CG所成的角的余弦值;
(3)求三棱锥G-CEF的体积.
(1)见解析 (2)EF与CG所成角的余弦值是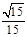 (3)
(3)
VG-CEF =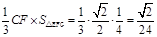
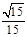 (3)
(3)VG-CEF =
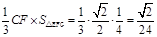
因此此几何休为正方体,易建立空间直角坐标系,用空间向量法解决。(1)只需证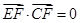 即可。
即可。
(2)用坐标借助公式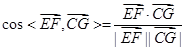 求EF与CG的所成角的余弦值。
求EF与CG的所成角的余弦值。
(3)利用三棱锥可换底的特性可其体积。即VG-CEF=VC-EFG.
建立如图所示的坐标系,则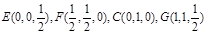 ……1分
……1分
(1)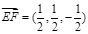 ,
,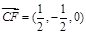 …………2分因为:
…………2分因为: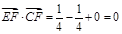 ……3分
……3分
所以: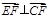 即:EF⊥CF……………4分
即:EF⊥CF……………4分

(2)因为: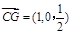
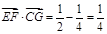 …………5分
…………5分
所以: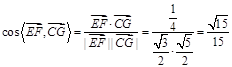 即:EF与CG所成角的余弦值是
即:EF与CG所成角的余弦值是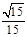
(3)CF⊥平面EFG,且CF=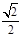 , S△EFG=
, S△EFG=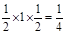 …………10分
…………10分
VG-CEF=VC-EFG=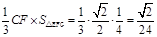
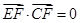 即可。
即可。(2)用坐标借助公式
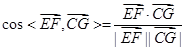 求EF与CG的所成角的余弦值。
求EF与CG的所成角的余弦值。(3)利用三棱锥可换底的特性可其体积。即VG-CEF=VC-EFG.
建立如图所示的坐标系,则
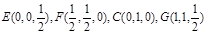 ……1分
……1分(1)
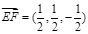 ,
,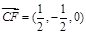 …………2分因为:
…………2分因为: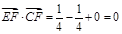 ……3分
……3分所以:
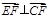 即:EF⊥CF……………4分
即:EF⊥CF……………4分
(2)因为:
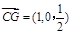
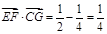 …………5分
…………5分所以:
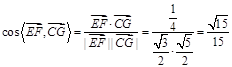 即:EF与CG所成角的余弦值是
即:EF与CG所成角的余弦值是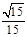
(3)CF⊥平面EFG,且CF=
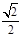 , S△EFG=
, S△EFG=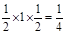 …………10分
…………10分VG-CEF=VC-EFG=
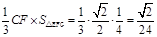

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
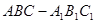 中,
中,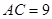 ,
,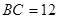 ,
,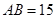 ,
,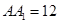 ,点D是
,点D是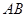 的中点.
的中点. 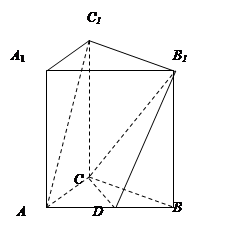
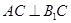 ;
;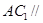 平面
平面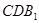 ;
; 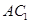 与直线
与直线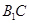 所成角的余弦值.
所成角的余弦值. 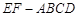 中,
中, 是梯形,
是梯形,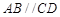 ,
, 是矩形,平面
是矩形,平面 平面
平面 ,
,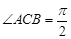 .
.
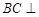 平面
平面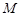 是棱
是棱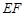 上一点,
上一点,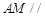 平面
平面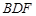 ,求
,求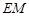 ;
;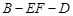 的平面角的余弦值.
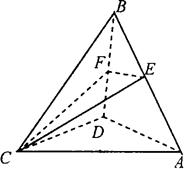
的平面角的余弦值.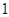 的正四面体
的正四面体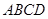 中,若
中,若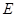 、
、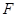 分别是棱
分别是棱 、
、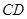 的中点,则
的中点,则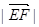 =
=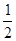
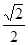
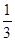
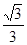
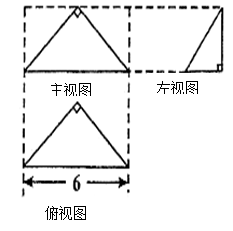
 ,那么这个三棱锥的体积是
,那么这个三棱锥的体积是 
