题目内容
【题目】设函数f(x)=ex-ax-2.
(1)求f(x)的单调区间;
(2)若a=1,k为整数,且当x>0时,(x-k)f′(x)+x+1>0,求k的最大值.
【答案】(1)当![]() 时,
时,![]() 的递增区间是
的递增区间是![]() ,当
,当![]() 时,
时,![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)求导得![]() ,
,![]() 函数单调递增,当
函数单调递增,当![]() 时,令
时,令![]() 得
得![]() ,所以函数
,所以函数![]() 上递减,
上递减,![]() 上递增;(2)当
上递增;(2)当![]() 时,原不等式分离参数后为
时,原不等式分离参数后为![]() ,利用导数右边函数最小值为
,利用导数右边函数最小值为![]() ,所以
,所以![]() 的最大值为
的最大值为![]() .
.
试题解析:
(1)f(x)的定义域为(-∞,+∞),f′(x)=ex-a.
若a≤0,则f′(x)>0,所以f(x)在(-∞,+∞)上单调递增.
若a>0,则当x∈(-∞,ln a)时,f′(x)<0;
当x∈(ln a,+∞)时,f′(x)>0.
所以,f(x)在(-∞,ln a)上单调递减,在(ln a,+∞)上单调递增.
(2)由于a=1时,(x-k)f′(x)+x+1=(x-k)(ex-1)+x+1.
故当x>0时,(x-k)f′(x)+x+1>0等价于
k<![]() +x(x>0)①
+x(x>0)①
令g(x)=![]() +x,则g′(x)=
+x,则g′(x)=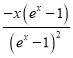 +1=
+1=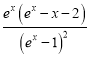 .
.
由(1)知,函数h(x)=ex-x-2在(0,+∞)上单调递增,
又h(1)=e-3<0,h(2)=e2-4>0.
所以h(x)在(0,+∞)上存在唯一零点.
故g′(x)在(0,+∞)上存在唯一零点.
设此零点为α,则α∈(1,2).
当x∈(0,α)时,g′(x)<0;当x∈(α,+∞)时,g′(x)>0,
所以g(x)在(0,+∞)上的最小值为g(α).
又由g′(α)=0,得eα=α+2, 所以g(α)=α+1∈(2,3).
由于①式等价于k<g(α),
故整数k的最大值为2.

【题目】衡州市临枣中学高二某小组随机调查芙蓉社区160个人,以研究这一社区居民在20:00-22:00时间段的休闲方式与性别的关系,得到下面的数据表:
休闲方式 性别 | 看电视 | 看书 | 合计 |
男 | 20 | 100 | 120 |
女 | 20 | 20 | 40 |
合计 | 40 | 120 | 160 |
下面临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
(Ⅰ)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量![]() ,求
,求![]() 的分别列和期望;
的分别列和期望;
(Ⅱ)根据以上数据,能否有99%的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
【题目】某初级中学有三个年级,各年级男、女人数如下表:
初一年级 | 初二年级 | 初三年级 | |
女生 | 370 |
| 200 |
男生 | 380 | 370 | 300 |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求![]() 的值;
的值;
(2)用分层抽样的方法在初三年级中抽取一个容量为5的样本,求该样本中女生的人数;
(3)用随机抽样的方法从初二年级女生中选出8人,测量它们的左眼视力,结果如下:1.2,1.5,1.2,1.5,1.5,1.3,1.0,1.2.把这8人的左眼视力看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.1的概率.