Question

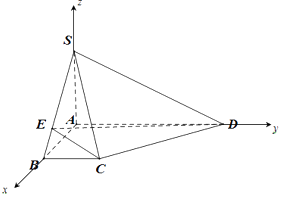
【题目】在如图所示的四棱锥S﹣ABCD中，SA⊥底面ABCD，∠DAB=∠ABC=90°，SA=AB=BC=a，AD=3a（a＞0），E为线段BS上的一个动点．

（1）证明：DE和SC不可能垂直；
（2）当点E为线段BS的三等分点（靠近B）时，求二面角S﹣CD﹣E的余弦值．

Answer 1

【答案】
（1）证明：∵SA⊥底面ABCD，∠DAB=90°，

∴AB、AD、AS两两垂直．故以A为原点，建立空间直角坐标系，如图

则S（0，0，a），C（a，a，0），D（0，3a，0）（a＞0），

∵SA=AB=a且SA⊥AB，

∴设E（x，0，a﹣x）其中0≤x≤a，

∴ ， ，

假设DE和SC垂直，则 ，

即ax﹣3a2﹣a2+ax=2ax﹣4a2=0，解得x=2a，

这与0≤x≤a矛盾，假设不成立，所以DE和SC不可能垂直

（2）解：∵E为线段BS的三等分点（靠近B），∴ ．

设平面SCD的一个法向量是 ，

∵ ， ，

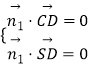∴ ，即 ，即 ，

取 ，

设平面CDE的一个法向量是 ，

∵ ， ，

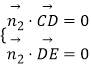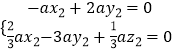∴ ，即 ，即 ，

取 ，

设二面角S﹣CD﹣E的平面角大小为θ，由图可知θ为锐角，

∴ ，

即二面角S﹣CD﹣E的余弦值为

【解析】由题可知，可以直接建立空间直角坐标线证明位置关系和计算角．（1）只要向量 恒成立，即可说明DE和SC不可能垂直；也可用反证法：假设DE与SC垂直，即 ，找出矛盾．（2）求出平面SCD和平面CDE的法向量，用向量角的余弦值来反应二面角的大小．
【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识，掌握相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点．