题目内容
【题目】设函数f(x)=|2x-1|+|2x-a|+a,x∈R.
(1)当a=3时,求不等式f(x)>7的解集;
(2)对任意x∈R恒有f(x)≥3,求实数a的取值范围.
【答案】(1) {x|x<0或x>2};(2) [2,+∞).
【解析】试题分析:(1)根据零点分段去掉绝对值写出函数的表达式,进而解出不等式;(2) 任意x∈R恒有f(x)≥3,即f(x)的最小值大于等于3,根据绝对值不等式求出最小值,解出a的范围.
试题解析:(1)当a=3时,f(x)=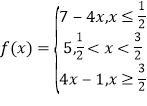
所以f(x)>7的解集为{x|x<0或x>2}.
(2)f(x)=|2x-1|+|a-2x|+a≥|2x-1+a-2x|+a=|a-1|+a,
由f(x)≥3恒成立,有|a-1|+a≥3,解得a≥2,
所以a的取值范围是[2,+∞).
点睛: 两数和差的绝对值的性质![]() ,特别注意此式,它是和差的绝对值与绝对值的和差性质,应用此式来求某些函数的最值时一定要注意等号成立的条件.
,特别注意此式,它是和差的绝对值与绝对值的和差性质,应用此式来求某些函数的最值时一定要注意等号成立的条件. ![]()
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]()
![]() .
.

练习册系列答案
相关题目