题目内容
某公司为了加大产品的宣传力度,准备立一块广告牌,在其背面制作一个形如△ABC的支架,要求∠ACB=60°,BC的长度大于2米,且AC比AB长1米.为节省材料,要求AC的长度越短越好,求AC的最短长度,且当AC最短时,BC的长度为多少米?

AC的最短长度为4+2 米,此时BC的长度为2+
米,此时BC的长度为2+ 米.
米.
 米,此时BC的长度为2+
米,此时BC的长度为2+ 米.
米.本试题主要考查了解三角形在实际生活中的运用。
解:设BC=x米(x>2),AC=y米,则AB=y-1.
在△ABC中,由余弦定理,得(y-1)2=y2+x2-2xycos60°.
所以y=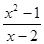 (x>2).……………8分
(x>2).……………8分
法一:y=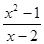 =(x-2)+
=(x-2)+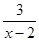 +4≥4+2
+4≥4+2 .
.
当且仅当x-2=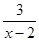 ,即x=2+
,即x=2+ 时,y有最小值4+2
时,y有最小值4+2 .
.
法二: y′=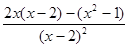 =
=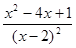 .
.
由y′=0得x=2+ .因为当2<x<2+
.因为当2<x<2+ 时,y′<0;当x>2+
时,y′<0;当x>2+ 时,y′>0,
时,y′>0,
所以当x=2+ 时,y有最小值4+2
时,y有最小值4+2 .
.
答:AC的最短长度为4+2 米,此时BC的长度为2+
米,此时BC的长度为2+ 米.……………15分
米.……………15分
解:设BC=x米(x>2),AC=y米,则AB=y-1.
在△ABC中,由余弦定理,得(y-1)2=y2+x2-2xycos60°.
所以y=
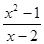 (x>2).……………8分
(x>2).……………8分法一:y=
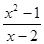 =(x-2)+
=(x-2)+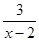 +4≥4+2
+4≥4+2 .
.当且仅当x-2=
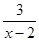 ,即x=2+
,即x=2+ 时,y有最小值4+2
时,y有最小值4+2 .
.法二: y′=
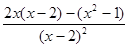 =
=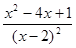 .
.由y′=0得x=2+
 .因为当2<x<2+
.因为当2<x<2+ 时,y′<0;当x>2+
时,y′<0;当x>2+ 时,y′>0,
时,y′>0,所以当x=2+
 时,y有最小值4+2
时,y有最小值4+2 .
.答:AC的最短长度为4+2
 米,此时BC的长度为2+
米,此时BC的长度为2+ 米.……………15分
米.……………15分
练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
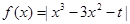
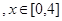 的最大值记为g(t),当t在实数范围内变化时g(t)最小值为
的最大值记为g(t),当t在实数范围内变化时g(t)最小值为 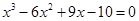 的实根个数是 ( )
的实根个数是 ( ) 在
在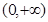 内有两个极值点,则实数
内有两个极值点,则实数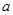 的取值范围是 ( )
的取值范围是 ( )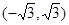
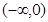
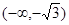
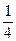
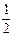
 ,若函数
,若函数 ,
, 有大于零的极值点,则( )
有大于零的极值点,则( )



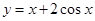 在区间
在区间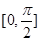 上的最大值是 。
上的最大值是 。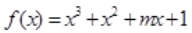 在R上无极值点,则实数m的取值范围是____.
在R上无极值点,则实数m的取值范围是____.