题目内容
4．已知P（x，y）是函数f（x）的图象上的一点，$\overrightarrow{a}$=（1，（x-2）5），$\overrightarrow{b}$=（1，y-2x），$\overrightarrow{a}$∥$\overrightarrow{b}$，数列{an}是公差不为零的等差数列，且f（a1）+f（a2）+…+f（a9）=36，则a1+a2+…+a9=18．分析 由向量共线的坐标表示求出函数f（x）的解析式，然后引入辅助函数g（x）=f（x+2），由其是奇函数结合已知及等差数列的性质得到a5=2，从而求得a1+a2+…+a9的值．
解答 解：∵$\overrightarrow{a}$=（1，（x-2）5），$\overrightarrow{b}$=（1，y-2x），由$\overrightarrow{a}$∥$\overrightarrow{b}$，得
y-2x-（x-2）5=0，即y=（x-2）5+2x，即f（x）=（x-2）5+2x，
令g（x）=f（x+2）-4=x5+2x，
则函数g（x）为奇函数，且是定义域内的增函数，
由f（a1）+f（a2）+…+f（a9）=36，
得g（a1-2）+g（a2-2）+…+g（a9-2）=0，
又数列{an}是公差不为0的等差数列，
∴g（a5-2）=0，即a5-2=0，a5=2，
∴a1+a2+…+a9=9a5=9×2=18．
故答案为：18．
点评 本题考查了平面向量平行的坐标运算，考查了函数的性质，考查了等差数列的性质，着重考查了数学转化思想方法的运用，属难题．
练习册系列答案
相关题目
12．已知矩形ABCD，AB=6，BC=4，经过A、B、C、D四顶点的椭圆（BC经过椭圆的焦点）的离心率是（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{1+\sqrt{10}}$ |
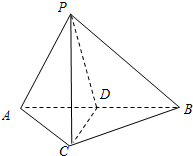如图，在三棱锥P-ABC中，AC=BC=2，∠ACB=90°，AP=BP=AB，PC⊥AC．