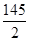题目内容
已知数列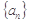 满足
满足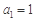 ,且
,且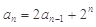 (n
(n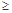 2且n∈N*).
2且n∈N*).
(Ⅰ)求数列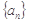 的通项公式;(5分)
的通项公式;(5分)
(Ⅱ)设数列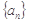 的前n项之和
的前n项之和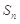 ,求
,求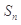 ,并证明:
,并证明: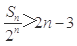 .(7分)
.(7分)
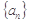 满足
满足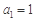 ,且
,且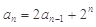 (n
(n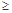 2且n∈N*).
2且n∈N*).(Ⅰ)求数列
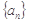 的通项公式;(5分)
的通项公式;(5分)(Ⅱ)设数列
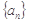 的前n项之和
的前n项之和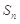 ,求
,求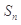 ,并证明:
,并证明: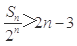 .(7分)
.(7分)(Ⅰ) .(Ⅱ)见解析
.(Ⅱ)见解析
 .(Ⅱ)见解析
.(Ⅱ)见解析(Ⅰ)根据已知式子构造关于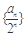 的递推式,从而利用数列的概念求出通项公式;(Ⅱ)利用错位相减法求出数列的前n项和,再利用不等式的性质证明不等式
的递推式,从而利用数列的概念求出通项公式;(Ⅱ)利用错位相减法求出数列的前n项和,再利用不等式的性质证明不等式
(Ⅰ)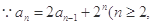 且n∈N*),
且n∈N*),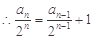 ,…2分
,…2分
即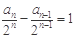 (
(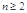 ,且
,且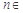 N*),所以,数列
N*),所以,数列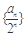 是等差数列,公差
是等差数列,公差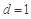 ,首项
,首项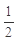 ,…3分
,…3分
于是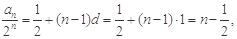
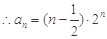 .……5分
.……5分
(Ⅱ)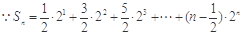 ①
①
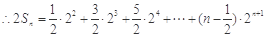 ②┈┈6分
②┈┈6分
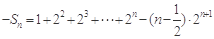
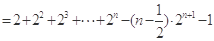
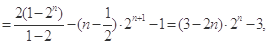 ………10分
………10分
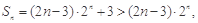
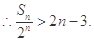
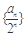 的递推式,从而利用数列的概念求出通项公式;(Ⅱ)利用错位相减法求出数列的前n项和,再利用不等式的性质证明不等式
的递推式,从而利用数列的概念求出通项公式;(Ⅱ)利用错位相减法求出数列的前n项和,再利用不等式的性质证明不等式(Ⅰ)
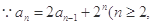 且n∈N*),
且n∈N*),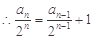 ,…2分
,…2分即
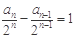 (
(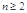 ,且
,且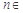 N*),所以,数列
N*),所以,数列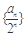 是等差数列,公差
是等差数列,公差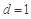 ,首项
,首项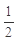 ,…3分
,…3分于是
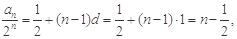
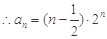 .……5分
.……5分(Ⅱ)
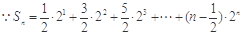 ①
① 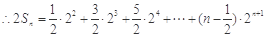 ②┈┈6分
②┈┈6分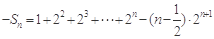
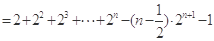
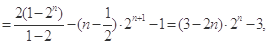 ………10分
………10分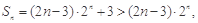
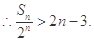

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
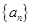 满足
满足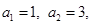
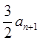 是
是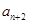 与
与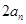 的等差中项
的等差中项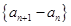 是等比数列;
是等比数列;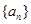 中,
中,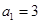 ,前
,前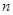 项和为
项和为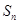 ,等比数列
,等比数列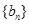 各项均为正数,
各项均为正数,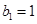 ,且
,且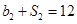 ,
,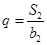
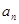 与
与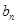 ;
;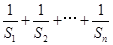
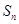 是数列
是数列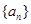 的前
的前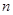 项和,且
项和,且
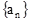 的通项公式;
的通项公式; 中,所有满足
中,所有满足 的正整数
的正整数 的个数称为这个数列
的个数称为这个数列 (n为正整数),求数列
(n为正整数),求数列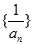 的前
的前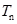 ,若
,若 对
对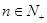 恒成立,求正整数
恒成立,求正整数 的最小值。
的最小值。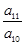 <-1,且它们的前n项和Sn有最大值,则使Sn>0的n的最大值为
<-1,且它们的前n项和Sn有最大值,则使Sn>0的n的最大值为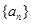 (公差不为零)和等差数列
(公差不为零)和等差数列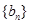 ,如果关于
,如果关于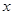 的方程
的方程 有解,那么以下九个方程已知等差数列
有解,那么以下九个方程已知等差数列 ,
, 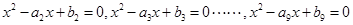 中,
中,

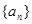 中,
中,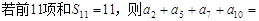 ( )
( )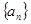 为等差数列,公差为
为等差数列,公差为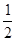 ,且
,且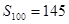 ,则
,则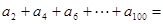 ( )
( )