题目内容
14.已知函数f(x)=x2-x+t,t≥0,g(x)=lnx.(1)令h(x)=f(x)+g(x),求证:h(x)是增函数;
(2)直线l与函数f(x),g(x)的图象都相切.对于确定的非负实数t,讨论直线l的条数,并说明理由.
分析 (1)利用导数判断函数的单调性即可;
(2)分别设出切点,再根导数的几何意义求出切线方程,构造方程组,消元,再构造函数F(x)=lnx+$\frac{(1+x)^{2}}{4{x}^{2}}$-(t+1),利用导数求出函数F(x)的最小值,再分类讨论,得到方程组的解得个数,继而得到切线的条数.
解答 解:(1)由h(x)=f(x)+g(x)=x2-x+t+lnx,得h'(x)=2x-1+$\frac{1}{x}$,x>0.
因为2x+$\frac{1}{x}$≥2$\sqrt{2x•\frac{1}{x}}$=2$\sqrt{2}$,所以h'(x)>0,
从而函数h(x)是增函数.
(2)记直线l分别切f(x),g(x)的图象于点(x1,x12-x1+t),(x2,lnx2),
由f'(x)=2x-1,得l的方程为y-(x12-x1+t)=(2x1-1)(x-x1),即y=(2x1-1)x-x12+t.
由g'(x)=$\frac{1}{x}$,得l的方程为y-lnx2=$\frac{1}{{x}_{2}}$(x-x2),即y=$\frac{1}{{x}_{2}}$•x+lnx2-1.
所以$\left\{\begin{array}{l}{2{x}_{1}-1=\frac{1}{{x}_{2}}}\\{-{{x}_{1}}^{2}+t=ln{x}_{2}-1}\end{array}\right.$(*)
消去x1得lnx2+$\frac{(1+{x}_{2})^{2}}{4{{x}_{2}}^{2}}$-(t+1)=0 (**).
令F(x)=lnx+$\frac{(1+x)^{2}}{4{x}^{2}}$-(t+1),则F'(x)=$\frac{1}{x}$-$\frac{1+x}{2{x}^{3}}$=$\frac{2{x}^{2}-x-1}{2{x}^{3}}$=$\frac{(2x+1)(x-1)}{2{x}^{3}}$,x>0.
由F'(x)=0,解得x=1.
当0<x<1时,F'(x)<0,当x>1时,F'(x)>0,
所以F(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
从而F(x)min=F(1)=-t.
当t=0时,方程(**)只有唯一正数解,从而方程组(*)有唯一一组解,
即存在唯一一条满足题意的直线;
当t>0时,F(1)<0,由于F(et+1)>ln(et+1)-(t+1)=0,
故方程(**)在(1,+∞)上存在唯一解;
令k(x)=lnx+$\frac{1}{x}$-1(x≤1),由于k'(x)=-$\frac{1}{x}$-$\frac{1}{{x}^{2}}$=$\frac{x-1}{{x}^{2}}$≤0,故k (x)在(0,1]上单调递减,
故当0<x<1时,k (x)>k (1)=0,即lnx>1-$\frac{1}{x}$,
从而lnx+$\frac{(1+x)^{2}}{4{x}^{2}}$-(t+1)>($\frac{1}{2x}$-$\frac{1}{2}$)2-t.
所以F($\frac{1}{2(\sqrt{t}+1)}$)>($\sqrt{t}$+$\frac{1}{2}$)2-t=$\sqrt{t}$+$\frac{1}{4}$>0,又0<$\frac{1}{2(\sqrt{t}+1)}$<1,
故方程(**)在(0,1)上存在唯一解.
所以当t>0时,方程(**)有两个不同的正数解,方程组(*)有两组解.即存在两条满足题意的直线.
综上,当t=0时,与两个函数图象同时相切的直线的条数为1;
当t>0时,与两个函数图象同时相切的直线的条数为2.
点评 本题考查了导数和函数的单调性质以及最值的关系,以及导数的几何意义方程组的解得个数问题,考查了学生转化能力,运算能力,属于难题.

 步步高达标卷系列答案
步步高达标卷系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 4n-1 | B. | 4n-1 | C. | 2n-1 | D. | 2n-1 |
 如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,AA1=$\sqrt{2}$a,E、F分别是AD、AB的中点.
如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,AA1=$\sqrt{2}$a,E、F分别是AD、AB的中点. 某校从参加高一年级期末考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题: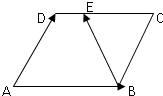 在边长为1的菱形ABCD中,∠A=60°,E是线段CD上一点,满足|$\overrightarrow{CE}$|=2||$\overrightarrow{DE}$|,如图所示,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
在边长为1的菱形ABCD中,∠A=60°,E是线段CD上一点,满足|$\overrightarrow{CE}$|=2||$\overrightarrow{DE}$|,如图所示,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.