题目内容
已知集合M={x|x+1＞0}，N={y|y=x2+1，x∈R}，则（ ）
| A、M⊆N | B、N⊆M | C、M∪N=R | D、M∩N=∅ |
考点：集合的包含关系判断及应用
专题：计算题,集合
分析：首先化简集合M，N，借助数轴，得出M，N的包含关系以及求出M，N的交集和并集．
解答：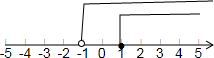
解：∵集合M={x|x+1＞0}={x|x＞-1}，
N={y|y=x2+1，x∈R}={y|y≥1}，
∴N⊆M，N?M，M∩N=N，M?N=M，
故A，C，D均错，B正确．
故选B．
解：∵集合M={x|x+1＞0}={x|x＞-1}，N={y|y=x2+1，x∈R}={y|y≥1}，
∴N⊆M，N?M，M∩N=N，M?N=M，
故A，C，D均错，B正确．
故选B．
点评：本题考查集合与集合的包含关系，以及集合的运算，求交集和并集，注意运用数轴求解．
练习册系列答案
相关题目
下列五种表示法：
①{x=2，y=1}；
②{（x，y）|
}；
③{（2，1）}；
④{2，1}；
⑤{（x，y）|x=2或y=1}；
能正确表示方程组
的解集是（ ）
①{x=2，y=1}；
②{（x，y）|
|
③{（2，1）}；
④{2，1}；
⑤{（x，y）|x=2或y=1}；
能正确表示方程组
|
| A、①②③④⑤ | B、②③④ |
| C、②③ | D、②③⑤ |
设集合A={x|x-2＜0}，集合B={x|x＞1}，则（ ）
| A、A⊆B | B、B⊆A | C、A∩B=∅ | D、A∩B≠∅ |
若集合A={x∈R|x-4|≤2}，非空集合B={x∈R|2a≤x≤a+3}，若B⊆A，则实数a的取值范围是（ ）
| A、（3，+∞） | B、[-1，+∞） | C、（1，3） | D、[1，3] |
R表示实数集，集合M={x|0≤x≤2}，N={x|x2-2x-3＞0}，则下列结论正确的是（ ）
| A、M⊆N | B、M⊆（∁RN） | C、（∁RM）⊆N | D、（∁RM）⊆（∁RN） |
已知集合M={2，a，b}，集合N={2a，2，b2}，且M=N，则a，b的值为（ ）
A、a=0，b=0或a=
| ||||
B、a=0，b=1或a=
| ||||
C、a=0，b=1或a=
| ||||
D、a=0，b=0或a=
|
集合A={x|-2＜x＜2}，B={x|-1≤x+2＜3}，那么A∪B=（ ）
| A、{x|-2＜x＜3} | B、{x|-3≤x＜2} | C、{x|-3≤x＜1} | D、{x|-2＜x≤1} |
设集合M={x|x2-3x-4＜0}，N={x|0≤x≤5}，则M∩N=（ ）
| A、（0，4] | B、[0，4） | C、[-1，0） | D、（-1，0] |