题目内容
下列五种表示法：
①{x=2，y=1}；
②{（x，y）|
}；
③{（2，1）}；
④{2，1}；
⑤{（x，y）|x=2或y=1}；
能正确表示方程组
的解集是（ ）
①{x=2，y=1}；
②{（x，y）|
|
③{（2，1）}；
④{2，1}；
⑤{（x，y）|x=2或y=1}；
能正确表示方程组
|
| A、①②③④⑤ | B、②③④ |
| C、②③ | D、②③⑤ |
考点：集合的表示法
专题：集合
分析：利用列举法和描述法可以表示集合，根据集合的表示方法进行判断即可．
解答：解：由于方程组
的解为
，
故方程组
的解集的描述法表示为：{（x，y）|
}；
方程组
的解集的列举法表示为{（2，1）}；
故选：C．
|
|
故方程组
|
|
方程组
|
故选：C．
点评：本题主要考查集合的含义和表示，利用集合元素的特点判断集合关系是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
设集合A={1，2，4}，集合B={x|x=a+b，a∈A，b∈A}，则集合B中有（ ）个元素．
| A、4 | B、5 | C、6 | D、7 |
由元素1，2，3组成的集合可记为（ ）
| A、{x=1，2，3} | B、{x=1，x=2，x=3} | C、{x|x∈N+，x＜4} | D、{6的质因数} |
不等式ax＞b的解集不可能是（ ）
| A、∅ | ||
| B、R | ||
C、（
| ||
D、（-∞，-
|
| 256 |
| A、{16} |
| B、{-16，16} |
| C、{4} |
| D、{-4，4} |
已知集合M={x|x+1＞0}，N={y|y=x2+1，x∈R}，则（ ）
| A、M⊆N | B、N⊆M | C、M∪N=R | D、M∩N=∅ |
设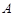
是由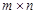
个实数组成的
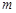行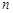
列的数表，如果某一行（或某一列）各数之和为负数，则改变该行（或该列）中所有数的符号，称为一次“操作”.
（1）数表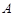如表1所示，若经过两“操”，使得到的数表每行的各数之和与每列的各数之和均为非负实数，请写出每次“操作”后所得的数表（写出一种方法即可）；表1
| 1 | 2 | 3 |  |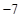
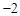 | 1 | 0 | 1 |
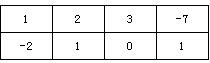
（2）数表
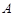如表2所示，若必须经过两次“操作”，才可使得到的数表每行的各数之和与每列的各数之和均为非负整数，求整数
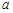的所有可能值；表2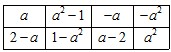
（3）对由
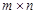个实数组成的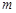行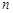列的任意一个数表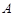，能否经过有限次“操作”以后，使得到的数表每行的各数之和与每列的各数之和均为非负实数？请说明理由.