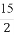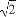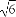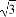题目内容
如图,在圆锥PO中,已知PO= ,☉O的直径AB=2,C是
,☉O的直径AB=2,C是 的中点,D为AC的中点.
的中点,D为AC的中点.

求证:平面POD⊥平面PAC.
见解析
【解析】
【证明】如图,以O为坐标原点,OB,OC,OP所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
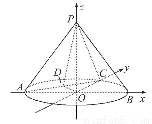
则O(0,0,0),A(-1,0,0),B(1,0,0),C(0,1,0),P(0,0,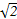 ),D(-
),D(-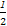 ,
,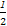 ,0).
,0).
设n1=(x1,y1,z1)是平面POD的一个法向量,则由n1·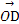 =0,n1·
=0,n1·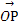 =0,
=0,
得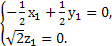
所以z1=0,x1=y1.取y1=1,得n1=(1,1,0).
设n2=(x2,y2,z2)是平面PAC的一个法向量,
则由n2·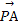 =0,
=0,
n2·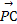 =0,得
=0,得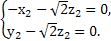
所以x2=-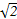 z2,y2=
z2,y2=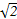 z2.
z2.
取z2=1,得n2=(-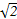 ,
,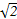 ,1).
,1).
因为n1·n2=(1,1,0)·(-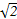 ,
,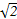 ,1)=0,
,1)=0,
所以n1⊥n2.
从而平面POD⊥平面PAC.

练习册系列答案
相关题目