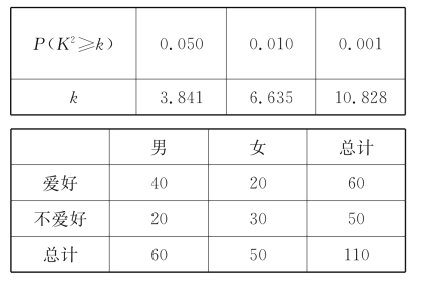
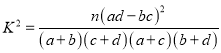题目内容
【题目】定义在R上的函数![]() 满足
满足![]() ,当
,当![]() 时总有
时总有![]()
![]() ,若
,若![]() ,则实数
,则实数![]() 的取值范围是_________.
的取值范围是_________.
【答案】![]()
【解析】
本题可先通过函数是偶函数将原不等式中的函数自变量转化为非负数,再利用函数的单调性研究,将不等式转化为两个自变量的大小比较,解不等式,得到本题结论.
∵定义在R上的函数f(x)满足f(﹣x)=f(x),
∴f(x)是偶函数,且f(﹣x)=f(x)=f(|x|).
∵当a,b∈(﹣∞,0)时总有![]() (a≠b),
(a≠b),
∴f(x)在(﹣∞,0)上单调递增,
∴f(x)在(0,+∞)上单调递减.
∵f(m+1)>f(2m),
∴f(|m+1|)>f(|2m|),
∴|m+1|<|2m|,
∴4m2>(m+1)2>0,
∴![]()
∴m<﹣![]() 或m>1.
或m>1.
∴实数m的取值范围是![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目