题目内容
【题目】如图,已知四边形ABCD为正方形,PD⊥平面ABCD且PD=AD,则下列命题中错误的是( )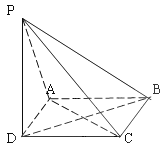
A.过BD且与PC平行的平面交PA于M点,则M为PA的中点
B.过AC且与PB垂直的平面交PB于N点,则N为PB的中点
C.过AD且与PC垂直的平面交PC于H点,则H为PC的中点
D.过P、B、C的平面与平面PAD的交线为直线l,则l∥AD
【答案】B
【解析】解:设AC∩BD=O,∵ABCD是正方形,∴O是AC中点,
∵过BD且与PC平行的平面交PA于M点,∴OM∥PC,
∴M是PA中点,故A正确;
设N为PB的中点,连结AN,
∵PA与AB不一定相等,∴AN与PB不一定垂直,
∴过AC且与PB垂直的平面交PB于N点,则N不一定是PB中点,故B错误;
∵四边形ABCD为正方形,PD⊥平面ABCD且PD=AD,
∴PA=AC,PD=DC,
∴过AD且与PC垂直的平面宛PC于H点,则H为PC的中点,故C正确;
∵AD∥BC,平面PAD与平面PCB有公共点P,
∴l∥AD∥BC,故D正确.
故选:B.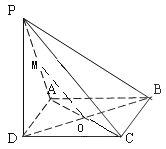
【考点精析】本题主要考查了直线与平面垂直的性质的相关知识点,需要掌握垂直于同一个平面的两条直线平行才能正确解答此题.

练习册系列答案
相关题目