题目内容
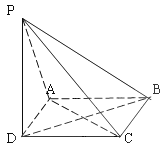
【题目】如图,矩形![]() 所在的平面与正方形
所在的平面与正方形![]() 所在的平面相互垂直,点
所在的平面相互垂直,点![]() 是
是![]() 的中点.
的中点.

(I)求证: ![]() 平面
平面![]() .
.
(II)求证:平面![]() 平面
平面![]() .
.
【答案】(I)见解析;(II)见解析.
【解析】试题分析:(1)要证线面平行,只须在平面内找到一条直线与这条直线平行,对本小题来说,连接![]() 交
交![]() 于点
于点![]() ,由三角形的中位线定理可证得
,由三角形的中位线定理可证得![]() ,问题得证;(2)要证面面垂直,只要在其中一个平面内找到一条直线与另一个平面垂直即可,由四边形
,问题得证;(2)要证面面垂直,只要在其中一个平面内找到一条直线与另一个平面垂直即可,由四边形![]() 为正方形且
为正方形且![]() 为对角线
为对角线![]() 的中点,所以有
的中点,所以有![]() ,故可考虑证明
,故可考虑证明![]() 平面
平面![]() ,故需要在平面
,故需要在平面![]() 内再找一条直线与
内再找一条直线与![]() 垂直即可,由平面
垂直即可,由平面![]() 平面
平面![]() ,交线为
,交线为![]() 且
且![]() ,从而
,从而![]() 平面
平面![]() ,可得
,可得![]() ,从而问题得证.
,从而问题得证.
试题解析:(1)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]()
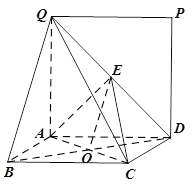
在三角形![]() 中,
中, ![]() ,
, ![]() 分别为
分别为![]() 和
和![]() 的中点
的中点
所以![]() ∥
∥![]() . 2分
. 2分
又![]() 平面
平面 ![]() ,
,![]() 平面
平面 ![]()
所以![]() ∥平面
∥平面![]() 4分
4分
(2)因为矩形![]() 所在的平面与正方形
所在的平面与正方形![]() 所在的平面相互垂直
所在的平面相互垂直
平面![]() 平面
平面 ![]() =
= ![]() ,
, ![]() ,
, ![]()
所以![]()
又![]() ,所以
,所以![]() 6分
6分
又因为![]() ,
, ![]() 是
是![]() 的中点,所以
的中点,所以![]()
又![]() ,所以
,所以![]() 7分
7分
由![]() ,所以平面
,所以平面![]() ⊥平面
⊥平面![]() 8分.
8分.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目