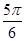题目内容
(本小题满分13分)
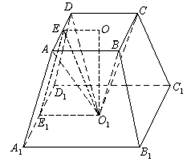
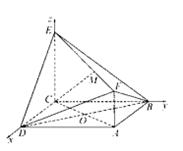
如图,已知正方形ABCD和梯形ACEF所在的平面互相垂直,
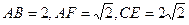 ,CE//AF,
,CE//AF,
(I)求证:CM//平面BDF;
(II)求异面直线CM与FD所成角的大小;
(III)求二面角A—DF—B的大小。
如图,已知正方形ABCD和梯形ACEF所在的平面互相垂直,
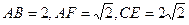 ,CE//AF,
,CE//AF,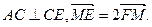
(I)求证:CM//平面BDF;
(II)求异面直线CM与FD所成角的大小;
(III)求二面角A—DF—B的大小。
|
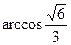 (Ⅲ)
(Ⅲ)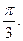
(I)证明:由题意可知CD、CB、CE两两垂直。
 可建立如图所示的空间直角坐标系
可建立如图所示的空间直角坐标系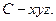
则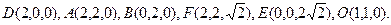 2分
2分
由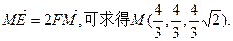 1分
1分
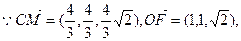
又 平面BDF,
平面BDF, 平面BDF。 2分
平面BDF。 2分
(Ⅱ)解:设异面直线CM与FD所成角的大小为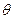
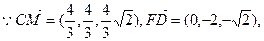
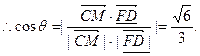
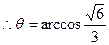 。
。
即异面直线CM与FD所成角的大小为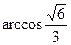 4分
4分
(III)解: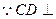 平面ADF,
平面ADF, 平面ADF的法向量为
平面ADF的法向量为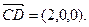 1分
1分
设平面BDF的法向量为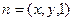 由
由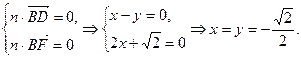
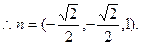 1分
1分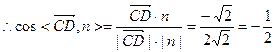
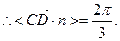 1分由图可知二面角A—DF—B的大小为
1分由图可知二面角A—DF—B的大小为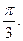 2分
2分
 可建立如图所示的空间直角坐标系
可建立如图所示的空间直角坐标系
则
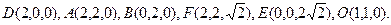 2分
2分由
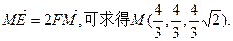 1分
1分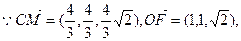
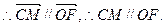
又
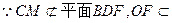 平面BDF,
平面BDF,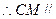 平面BDF。 2分
平面BDF。 2分(Ⅱ)解:设异面直线CM与FD所成角的大小为
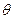
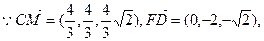
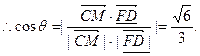
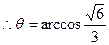 。
。即异面直线CM与FD所成角的大小为
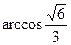 4分
4分(III)解:
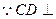 平面ADF,
平面ADF,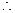 平面ADF的法向量为
平面ADF的法向量为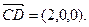 1分
1分设平面BDF的法向量为
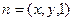 由
由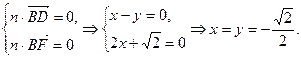
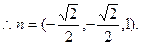 1分
1分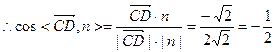
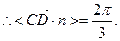 1分由图可知二面角A—DF—B的大小为
1分由图可知二面角A—DF—B的大小为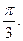 2分
2分
练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
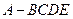 中,底面
中,底面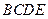 为矩形,侧面
为矩形,侧面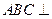 底面
底面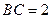 ,
,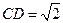 ,
,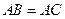 。
。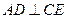 ;
;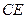 与平面
与平面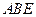 所成的角为
所成的角为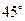 ,求二面角
,求二面角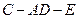 的大小。
的大小。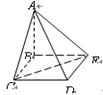
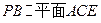 ;
;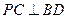 ;
; 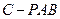 的体积.
的体积.
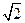 ,AC=3,BC=
,AC=3,BC=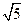 ,D是A1C的中点E是侧棱BB1上的一动点。
,D是A1C的中点E是侧棱BB1上的一动点。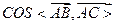 的值
的值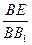 的值,不存在则说明理由。
的值,不存在则说明理由。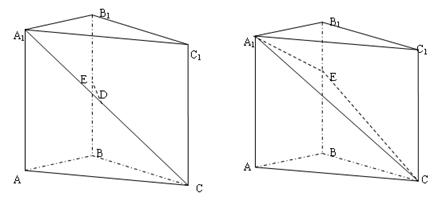
 ,的棱长为1,
,的棱长为1,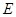 为
为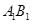 的中点,则下列五个命题:
的中点,则下列五个命题: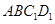 ,的距离为
,的距离为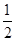
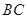 与平面
与平面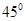
 ,在正方体六个面内形成六个射影,其面积的最小值是
,在正方体六个面内形成六个射影,其面积的最小值是 与
与 所成的角
所成的角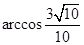
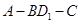 的大小为
的大小为