题目内容
已知抛物线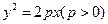 的焦点为
的焦点为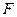 ,过
,过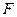 的直线交
的直线交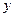 轴正半轴于点
轴正半轴于点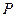 ,交抛物线于
,交抛物线于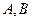 两点,其中点
两点,其中点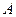 在第一象限.
在第一象限.
(Ⅰ)求证:以线段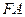 为直径的圆与
为直径的圆与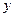 轴相切;
轴相切;
(Ⅱ)若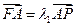 ,
,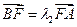 ,
,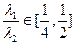 ,求
,求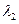 的取值范围.
的取值范围.
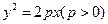 的焦点为
的焦点为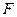 ,过
,过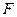 的直线交
的直线交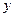 轴正半轴于点
轴正半轴于点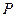 ,交抛物线于
,交抛物线于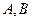 两点,其中点
两点,其中点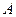 在第一象限.
在第一象限.(Ⅰ)求证:以线段
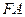 为直径的圆与
为直径的圆与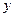 轴相切;
轴相切;(Ⅱ)若
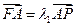 ,
,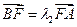 ,
,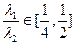 ,求
,求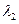 的取值范围.
的取值范围.解:(Ⅰ)由已知 ,设
,设 ,则
,则 ,
,
圆心坐标为 ,圆心到
,圆心到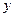 轴的距离为
轴的距离为 , …………………2分
, …………………2分
圆的半径为 , …………………4分
, …………………4分
所以,以线段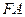 为直径的圆与
为直径的圆与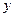 轴相切. …………………5分
轴相切. …………………5分
(Ⅱ)解法一:设 ,由
,由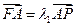 ,
,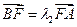 ,得
,得
 ,
, , …………………6分
, …………………6分
所以 ,
,
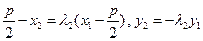 , …………………8分
, …………………8分
由 ,得
,得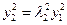 .
.
又 ,
, ,
,
所以 . …………………10分
. …………………10分
代入 ,得
,得 ,
,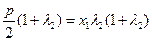 ,
,
整理得 , …………………12分
, …………………12分
代入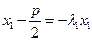 ,得
,得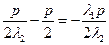 ,
,
所以 , …………………13分
, …………………13分
因为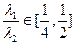 ,所以
,所以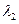 的取值范围是
的取值范围是 . …………………14分
. …………………14分
解法二:设 ,
,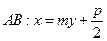 ,
,
将 代入
代入 ,得
,得 ,
,
所以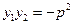 (*), …………………6分
(*), …………………6分
由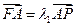 ,
,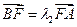 ,得
,得
 ,
, , …………………7分
, …………………7分
所以, ,
,
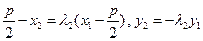 , …………………8分
, …………………8分
将 代入(*)式,得
代入(*)式,得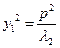 , …………………10分
, …………………10分
所以 ,
, . …………………12分
. …………………12分
代入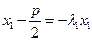 ,得
,得 . …………………13分
. …………………13分
因为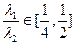 ,所以
,所以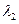 的取值范围是
的取值范围是 . …………………14分
. …………………14分
 ,设
,设 ,则
,则 ,
,圆心坐标为
 ,圆心到
,圆心到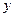 轴的距离为
轴的距离为 , …………………2分
, …………………2分圆的半径为
 , …………………4分
, …………………4分所以,以线段
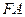 为直径的圆与
为直径的圆与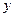 轴相切. …………………5分
轴相切. …………………5分(Ⅱ)解法一:设
 ,由
,由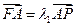 ,
,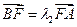 ,得
,得 ,
, , …………………6分
, …………………6分所以
 ,
,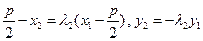 , …………………8分
, …………………8分由
 ,得
,得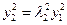 .
.又
 ,
, ,
,所以
 . …………………10分
. …………………10分代入
 ,得
,得 ,
,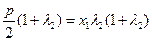 ,
,整理得
 , …………………12分
, …………………12分代入
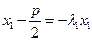 ,得
,得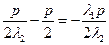 ,
,所以
 , …………………13分
, …………………13分因为
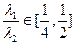 ,所以
,所以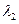 的取值范围是
的取值范围是 . …………………14分
. …………………14分解法二:设
 ,
,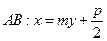 ,
,将
 代入
代入 ,得
,得 ,
,所以
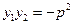 (*), …………………6分
(*), …………………6分由
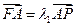 ,
,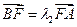 ,得
,得 ,
, , …………………7分
, …………………7分所以,
 ,
,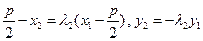 , …………………8分
, …………………8分将
 代入(*)式,得
代入(*)式,得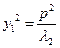 , …………………10分
, …………………10分所以
 ,
, . …………………12分
. …………………12分代入
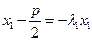 ,得
,得 . …………………13分
. …………………13分因为
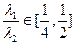 ,所以
,所以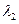 的取值范围是
的取值范围是 . …………………14分
. …………………14分略

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
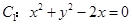 与曲线
与曲线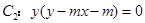 有四个不同的交点,则实数
有四个不同的交点,则实数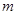 的取值范围是 ( )
的取值范围是 ( )



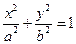 (
(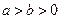 )的焦距为
)的焦距为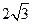 ,离心率为
,离心率为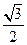 .
.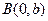 ,斜率为
,斜率为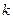 的直线交椭圆于另一点
的直线交椭圆于另一点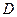 ,交
,交 轴于点
轴于点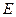 ,且
,且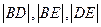 成等比数列,求
成等比数列,求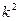 的值.
的值.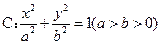 的左,右顶点,
的左,右顶点,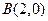 ,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线
,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线 于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点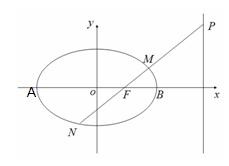
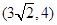 到两焦点的距离之和是12,则椭圆的标准方程是 .
到两焦点的距离之和是12,则椭圆的标准方程是 .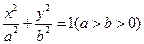 的焦点分别为
的焦点分别为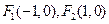 ,
,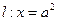 交
交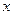 轴于于点A,且
轴于于点A,且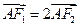 。
。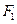 、
、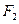 分别作互相垂直的两直线与椭圆分别
分别作互相垂直的两直线与椭圆分别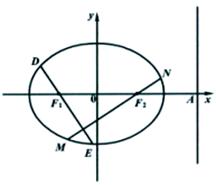
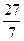 ,求DE的直线方程。
,求DE的直线方程。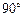 ,AC=2)沿x轴滚动,设顶点A(x,y)的轨迹方程是y=
,AC=2)沿x轴滚动,设顶点A(x,y)的轨迹方程是y=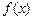 ,则
,则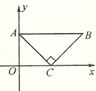
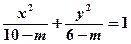 与曲线
与曲线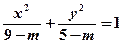 具有相同的焦距,则
具有相同的焦距,则 的取值范围是
的取值范围是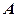 .
.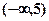
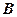 .
.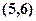
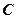 .
.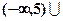
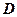 .
.
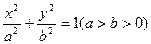 的左焦点
的左焦点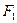 ,O为坐标原点,点P在椭圆上,点Q在椭圆的右准线上,若
,O为坐标原点,点P在椭圆上,点Q在椭圆的右准线上,若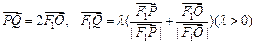 则椭圆的离心率为
则椭圆的离心率为  .
.