题目内容
已知双曲线 的两个焦点分别为
的两个焦点分别为 、
、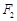 ,则满足△
,则满足△ 的周长为
的周长为 的动点
的动点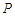 的轨迹方程为 ( )
的轨迹方程为 ( )
 的两个焦点分别为
的两个焦点分别为 、
、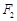 ,则满足△
,则满足△ 的周长为
的周长为 的动点
的动点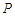 的轨迹方程为 ( )
的轨迹方程为 ( )A. | B. | C. | D. |
C
试题分析:根据已知双曲线方程,运用公式可得它的两个焦点分别为F1(0,-
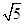 )、F2(0,
)、F2(0,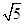 ).再根据△PF1F2的周长为6+2
).再根据△PF1F2的周长为6+2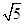 ,结合椭圆的定义得到点P的轨迹是以F1、F2为焦点的椭圆,因为三角形三顶点不能共线,所以上、下顶点除外.由椭圆的定义求得椭圆的长半轴、短半轴分别为3和2.因此可得椭圆的标准方程,得到正确选项.
,结合椭圆的定义得到点P的轨迹是以F1、F2为焦点的椭圆,因为三角形三顶点不能共线,所以上、下顶点除外.由椭圆的定义求得椭圆的长半轴、短半轴分别为3和2.因此可得椭圆的标准方程,得到正确选项.因为双曲线
 ,因此可知其两个焦点分别为F1(0,-
,因此可知其两个焦点分别为F1(0,-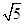 )、F2(0,
)、F2(0,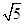 ).
).因为△
 的周长为
的周长为 ,
, ,那么说明了动点
,那么说明了动点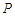 的轨迹是以
的轨迹是以 、
、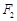 为焦点的椭圆,则由椭圆的定义得到,长轴长为6,长半轴为3,短半轴长为2,故可知P的轨迹方程为
为焦点的椭圆,则由椭圆的定义得到,长轴长为6,长半轴为3,短半轴长为2,故可知P的轨迹方程为 ,同时去掉上下顶点。选C.
,同时去掉上下顶点。选C.点评:该试题着重考查了椭圆、双曲线等圆锥曲线的标准方程,以及简单的轨迹方程求法等知识点,属于中档题.那么求轨迹方程 方法一般是考虑定义法和直接法来求解的比较多。

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
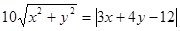 ,则动点M的轨迹方程是
,则动点M的轨迹方程是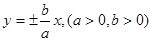 ,若双曲线上有一点M(
,若双曲线上有一点M(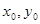 ),使
),使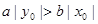 ,那双曲线的交点( )。
,那双曲线的交点( )。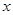 轴上
轴上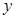 轴上
轴上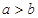 时在
时在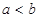 时在
时在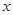 轴上的椭圆
轴上的椭圆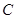 过点
过点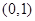 ,且离心率为
,且离心率为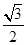 ,
,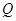 为椭圆
为椭圆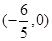 的直线
的直线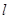 与椭圆
与椭圆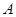 ,
,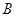 两点.
两点.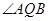 的大小;
的大小;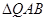 为等腰三角形?如果存在,求出直线
为等腰三角形?如果存在,求出直线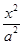 +
+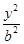 =1(a>b>0)的一个焦点是F(1,0),且离心率为
=1(a>b>0)的一个焦点是F(1,0),且离心率为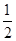 .
.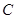 方程为
方程为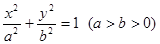 ,左、右焦点分别是
,左、右焦点分别是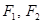 ,若椭圆
,若椭圆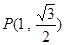 到
到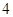 .
. 是椭圆
是椭圆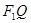 中点
中点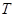 的轨迹方程;
的轨迹方程;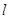 过定点
过定点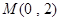 ,且与椭圆
,且与椭圆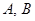 ,若
,若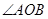 为锐角(
为锐角( 为坐标原点),求直线
为坐标原点),求直线 的取值范围.
的取值范围.
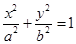 (
(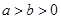 )的一个顶点为
)的一个顶点为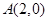 ,离心率为
,离心率为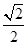 ,直线
,直线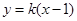 与椭圆
与椭圆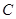 交于不同的两点
交于不同的两点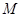 、
、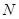 .(1) 求椭圆
.(1) 求椭圆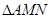 的面积为
的面积为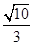 时,求
时,求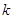 的值.
的值.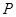 是椭圆
是椭圆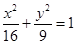 上的点,
上的点, 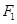 、
、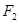 是椭圆的两个焦点,则
是椭圆的两个焦点,则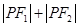 的值为
的值为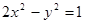 的右支交于不同的两点A,B
的右支交于不同的两点A,B