题目内容
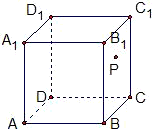如图，在正方体ABCD-A1B1C1D1中，P是侧面BB1C1C内一动点，若P到直线BC与直线C1D1的距离相等，则动点P的轨迹所在的曲线是
- A.直线
- B.圆
- C.双曲线
- D.抛物线
D
分析：由线C1D1垂直平面BB1C1C，分析出|PC1|就是点P到直线C1D1的距离，则动点P满足抛物线定义，问题解决．
解答：由题意知，直线C1D1⊥平面BB1C1C，则C1D1⊥PC1，即|PC1|就是点P到直线C1D1的距离，
那么点P到直线BC的距离等于它到点C的距离，所以点P的轨迹是抛物线．
故选D．
点评：本题考查抛物线定义及线面垂直的性质．
分析：由线C1D1垂直平面BB1C1C，分析出|PC1|就是点P到直线C1D1的距离，则动点P满足抛物线定义，问题解决．
解答：由题意知，直线C1D1⊥平面BB1C1C，则C1D1⊥PC1，即|PC1|就是点P到直线C1D1的距离，
那么点P到直线BC的距离等于它到点C的距离，所以点P的轨迹是抛物线．
故选D．
点评：本题考查抛物线定义及线面垂直的性质．
练习册系列答案
相关题目
若Rt△ABC中两直角边为a、b，斜边c上的高为h，则
如图，在正方体的一角上截取三棱锥P-ABC，PO为棱锥的高，记
若Rt△ABC中两直角边为a、b，斜边c上的高为h，则
如图，在正方体ABCD-A1B1C1D1中，E为DD1的中点，
如图，在正方体ABCD-A1B1C1D1中，点P是上底面A1B1C1D1内一动点，则三棱锥P-ABC的主视图与左视图的面积的比值为（ ）