题目内容
已知数列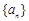 的前
的前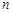 项和为
项和为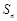 满足
满足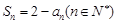 .
.
(Ⅰ)求数列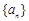 的通项公式;
的通项公式;
(Ⅱ)求数列 的前
的前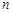 项和
项和 .
.
(Ⅰ) ;(Ⅱ)
;(Ⅱ)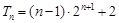 .
.
解析试题分析:(Ⅰ)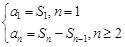 ,由
,由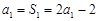 ,得
,得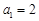 ,当
,当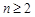 时,有
时,有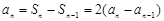 ,
,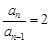 再根据等比数列的定义可求出
再根据等比数列的定义可求出 ;
;
(Ⅱ)由(Ⅰ)可知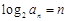 ,得到
,得到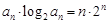 ,再利用错位相减法求
,再利用错位相减法求 的前
的前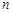 项和
项和 ,
,
由题意得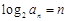 ,所以
,所以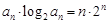 得
得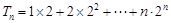 记为①,对①两边同时乘以数列
记为①,对①两边同时乘以数列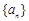 的公比2,得到②式
的公比2,得到②式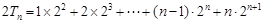 ,利用错位相减得到
,利用错位相减得到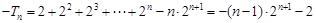 ,化简得
,化简得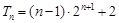 .
.
试题解析:(1)由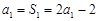 ,得
,得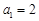
当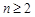 时,有
时,有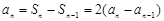 ,
,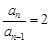
所以数列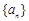 是以2为首项,2为公比的等比数列,所以
是以2为首项,2为公比的等比数列,所以
(2)由题意得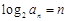 ,所以
,所以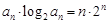
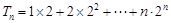 ……………………………………①
……………………………………①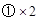 得
得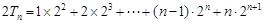 …………②
…………②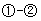 得
得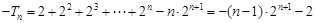 ,所以
,所以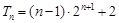 .
.
考点:1.数列的递推关系;2.等比数列的性质;3.数列的前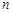 项和求法.
项和求法.

练习册系列答案
相关题目
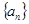 的前n项的和为
的前n项的和为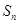 ,且
,且 ,
,
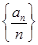 是等比数列
是等比数列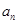 与前n项的和
与前n项的和 若集合M=
若集合M= 恰有4个元素,求实数
恰有4个元素,求实数 的取值范围.
的取值范围.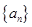 的前
的前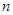 项和为
项和为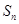 ,
,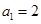 ,
,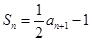
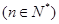 .
.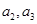 ;
;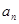 ;
;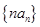 的前
的前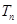 .
.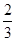 an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.
an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.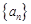 的前
的前 项和
项和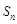 满足
满足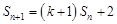 ,又
,又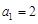 ,
,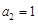 .
.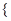 an
an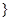 为等比数列,它的前n项和为Sn,a1=1,且
为等比数列,它的前n项和为Sn,a1=1,且 .
. 的通项公式;
的通项公式;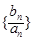 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列 的前n项和Tn.
的前n项和Tn.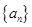 的前
的前 项和为
项和为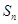 ,数列
,数列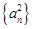 的前
的前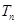 ,且
,且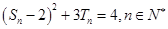 .
.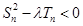 对
对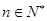 恒成立,求
恒成立,求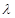 的最小值;
的最小值;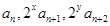 成等差数列,求正整数
成等差数列,求正整数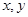 的值.
的值. 的前
的前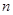 项和
项和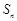 满足:
满足: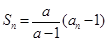 (
(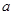 为常数,且
为常数,且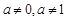 ).
). 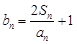 ,若数列
,若数列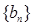 为等比数列,求
为等比数列,求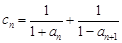 ,数列
,数列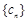 的前
的前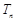 ,求证:
,求证: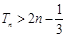 .
.