题目内容
已知各项均为正数的数列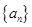 的前
的前 项和为
项和为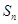 ,数列
,数列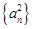 的前
的前 项和为
项和为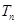 ,且
,且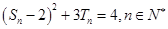 .
.
⑴证明:数列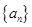 是等比数列,并写出通项公式;
是等比数列,并写出通项公式;
⑵若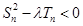 对
对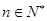 恒成立,求
恒成立,求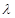 的最小值;
的最小值;
⑶若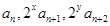 成等差数列,求正整数
成等差数列,求正整数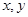 的值.
的值.
(1)证明见解析,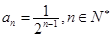 ;(2)3;(3)
;(2)3;(3)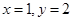
解析试题分析:(1)要证数列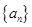 是等比数列,可根据题设求出
是等比数列,可根据题设求出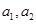 ,当然也可再求
,当然也可再求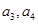 ,虽然得出的
,虽然得出的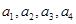 成等比数列,但前面有限项成等比不能说明所有项都成等比,必须严格证明.一般方法是把已知式
成等比数列,但前面有限项成等比不能说明所有项都成等比,必须严格证明.一般方法是把已知式 中的
中的 用
用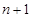 代换得到
代换得到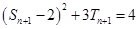 ,两式相减得
,两式相减得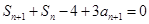 ,这个式子中把
,这个式子中把 用
用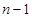 代换又得
代换又得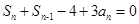 ,两式再相减,正好得出数列的前后项关系的递推关系
,两式再相减,正好得出数列的前后项关系的递推关系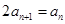 ,正是等比数列的表现.(2)由题间
,正是等比数列的表现.(2)由题间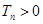 ,对不等式
,对不等式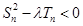 用分离参数法得
用分离参数法得 ,求
,求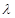 的最小值就与求
的最小值就与求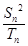 的最大值(也只要能是取值范围)联系起来了.(3)只能由
的最大值(也只要能是取值范围)联系起来了.(3)只能由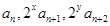 成等差数列列出唯一的等式,这个等式是关于
成等差数列列出唯一的等式,这个等式是关于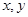 的二元方程,它属于不定方程,有无数解,只是由于
的二元方程,它属于不定方程,有无数解,只是由于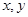 都是正整数,利用正整数的性质可得出具体的解.
都是正整数,利用正整数的性质可得出具体的解.
试题解析:(1)当n=1时,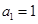 ;当n=2时,
;当n=2时,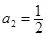
当n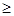 3时,有
3时,有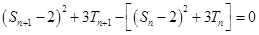 得:
得:
化简得: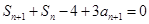 3分
3分
又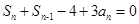 ∴
∴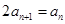
∴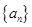 是1为首项,
是1为首项,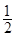 为公比的等比数列
为公比的等比数列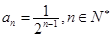 6分
6分
(2)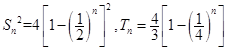
∴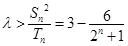 ∴
∴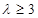 11分
11分
(3)若三项成等差,则有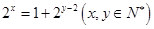
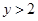 ,右边为大于2的奇数,左边为偶数或1,不成立
,右边为大于2的奇数,左边为偶数或1,不成立
∴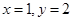 16分
16分
考点:(1)等比数列的通项公式;(2)不等式恒成立与函数的最值;(3)不定方程的正整数解问题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 ,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数.
,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数.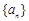 的前
的前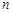 项和为
项和为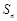 满足
满足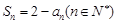 .
. 的前
的前 .
. }的前n项和为
}的前n项和为 ,
,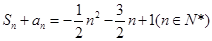 .
.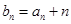 ,证明:数列
,证明:数列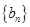 是等比数列;
是等比数列;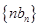 的前
的前 项和
项和 ;
;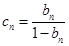 ,数列
,数列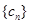 的前
的前
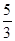 .
.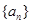 是公比大于1的等比数列,
是公比大于1的等比数列,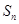 为数列
为数列 项和.已知
项和.已知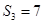 ,且
,且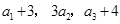 构成等差数列.
构成等差数列.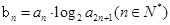 ,求数列
,求数列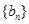 的前n项和
的前n项和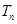 .
.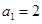 ,
,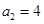 ,数列
,数列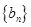 满足:
满足: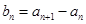 ,
,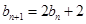 .
. 是等比数列(要指出首项与公比);
是等比数列(要指出首项与公比);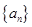 的通项公式.
的通项公式. 的前n项和为
的前n项和为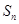 ,
,
 是等比数列;
是等比数列; ,数列
,数列 的前n项和为
的前n项和为 ,求不超过
,求不超过 的最大整数的值.
的最大整数的值.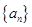 中,
中, .
.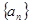 通项公式;
通项公式; ,求证:
,求证: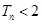 .
.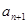 ,
,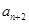 …的最小值记为Bn,dn=An-Bn.
…的最小值记为Bn,dn=An-Bn.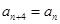 ),写出d1,d2,d3,d4的值;
),写出d1,d2,d3,d4的值;