题目内容
已知函数 在区间
在区间 上是减函数,那么
上是减函数,那么 ( )
( )
A.有最小值 | B.有最大值 |
C.有最小值 | D.有最大值 |
D
解析试题分析:由f(x)在[-1,2]上是减函数,知f′(x)=3x2+2bx+c≤0,x∈[-1,2],
则f′(-1)=3-2b+c≤0,且f′(2)=12+4b+c≤0,⇒15+2b+2c≤0⇒b+c≤- ,故选D.
,故选D.
考点:本题主要考查了函数的单调性与其导函数的正负情况之间的关系,即导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.
点评:解决该试题的关键是先对函数f(x)求导,然后令导数在[-1,2]小于等于0即可求出b+c的关系,得到答案.

练习册系列答案
相关题目
具有性质: 的函数,我们称为满足“倒负”变换的函数,下列函数:①
的函数,我们称为满足“倒负”变换的函数,下列函数:① ;②
;② ;③
;③ 中满足“倒负”变换的函数是( )
中满足“倒负”变换的函数是( )
| A.①② | B.①③ | C.②③ | D.只有① |
若函数
A. | B. |
C. | D. |
设f(x)是R上的奇函数,且当x>0时,f(x)=x(1+ ),则当x<0时,f(x)=( )
),则当x<0时,f(x)=( )
A.-x(1+ ) ) | B.x(1+ ) ) | C.-x(1- ) ) | D. x(1- ) ) |
设函数
 的图象关于直线
的图象关于直线 及直线
及直线 对称,且
对称,且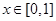 时,
时, ,则
,则 ( )
( )
A. | B. | C. | D. |
已知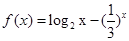 ,若实数
,若实数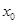 是方程
是方程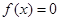 的解,且
的解,且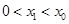 ,则
,则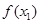 的值是( )
的值是( )
| A.恒为负 | B.等于零 | C.恒为正 | D.不小于零 |
下列四个函数,不在区间[1,2]上单调递减的是
A.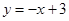 | B.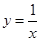 | C.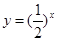 | D.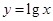 |

 )
) 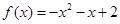 ,则函数
,则函数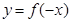 的图象为( )
的图象为( )