题目内容
设函数
 的图象关于直线
的图象关于直线 及直线
及直线 对称,且
对称,且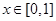 时,
时, ,则
,则 ( )
( )
A. | B. | C. | D. |
B
解析试题分析:因为函数y=f(x)关于直线x=0对称说明函数是偶函数,同时关于x=1对称,说明了f(2-x)=f(x),那么由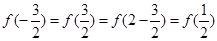 ,然后将变量代入函数解析式中可知,
,然后将变量代入函数解析式中可知,  ,故选B.
,故选B.
考点:本试题主要考查了函数的对称性的运用,以及奇偶性的综合问题。
点评:解决该试题的关键是分析得到函数是偶函数,同时关于直线x=1对称,得到关系式f(2-x)=f(x),进而求解得到。

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
函数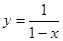 的图像与函数
的图像与函数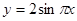 (
(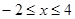 )的图像所有交点的横坐标之和等于 ( )
)的图像所有交点的横坐标之和等于 ( )
| A.2 | B.4 | C.6 | D.8 |
若R上的奇函数 的图象关于直线
的图象关于直线 对称,且当
对称,且当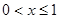 时,
时, ,则方程
,则方程 在区间
在区间 内的所有实数根之和为( )
内的所有实数根之和为( )
| A.4020 | B.4022 | C.4024 | D.4026 |
设 ,则
,则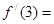 为( )
为( )
A. | B. | C. | D. |
函数 的定义域为
的定义域为
A. | B. | C. | D. |
已知函数 在区间
在区间 上是减函数,那么
上是减函数,那么 ( )
( )
A.有最小值 | B.有最大值 |
C.有最小值 | D.有最大值 |
下列函数中,既是奇函数又是增函数的为
A. | B. | C. | D. |
设函数 的定义域为M,函数
的定义域为M,函数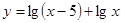 的定义域为N,则( )
的定义域为N,则( )
| A.M∪N=R | B.M="N" | C.M N N | D.M N N |
 与
与 的图象可能是( )
的图象可能是( )


