题目内容
设f(x)是R上的奇函数,且当x>0时,f(x)=x(1+ ),则当x<0时,f(x)=( )
),则当x<0时,f(x)=( )
A.-x(1+ ) ) | B.x(1+ ) ) | C.-x(1- ) ) | D. x(1- ) ) |
D
解析试题分析:因为f(x)是R上的奇函数,且当x<0时,-x>0,那么代入已知解析式中,得到f(-x)=-x(1+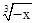 )=-f(x),可知f(x)= x(1+
)=-f(x),可知f(x)= x(1+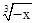 ),可知答案为D.
),可知答案为D.
考点:本题主要考查了奇偶性定义及选择题的解法,同时考查求函数的值等有关知识,属于基础题.
点评:解决该试题的关键是利用奇函数的定义,那么结合对称性,将x<0的变量转化为x>0的区域,结合已知的解析式求解得到。

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
设函数 的图像的交点为
的图像的交点为 ,则x0所在的区间是
,则x0所在的区间是
A. | B. | C. | D. |
函数 的定义域是( ).
的定义域是( ).
A. | B. | C. | D. |
已知函数 的图象如图所示,则
的图象如图所示,则 满足的关系是( )
满足的关系是( )
A. | B. |
C. | D. |
设 ,则
,则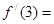 为( )
为( )
A. | B. | C. | D. |
已知函数 在区间
在区间 上是减函数,那么
上是减函数,那么 ( )
( )
A.有最小值 | B.有最大值 |
C.有最小值 | D.有最大值 |
已知函数 ,则
,则 是( )
是( )
| A.奇函数 | B.偶函数 |
| C.既是奇函数又是偶函数 | D.非奇函数非偶函数 |
已知 其中
其中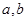 为常数,若
为常数,若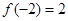 ,则
,则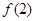 =( )
=( )
| A.2 | B.-6 | C.-10 | D.-4 |
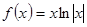 的大致图象是
的大致图象是