题目内容
若函数
A. | B. |
C. | D. |
B
解析试题分析:令 ,则
,则 ,所以
,所以 ,即
,即 。
。
考点:本题考查函数解析式的求法。
点评:若已知复合函数f[g(x)]的解析式,求函数f(x)的解析式,常用换元法。令g(x)=" t" ,求f(t)的解析式,然后t换为x即可。 但要注意换元后,应再求新变量的取值范围,即为函数的定义域。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数 的单调递减区间是 ( )
的单调递减区间是 ( )
A. | B. | C. | D. |
函数 对任意的
对任意的 恒有
恒有 且
且 ,则
,则 ( )
( )
A. | B. | C. | D. |
函数 的定义域是( ).
的定义域是( ).
A. | B. | C. | D. |
若R上的奇函数 的图象关于直线
的图象关于直线 对称,且当
对称,且当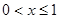 时,
时, ,则方程
,则方程 在区间
在区间 内的所有实数根之和为( )
内的所有实数根之和为( )
| A.4020 | B.4022 | C.4024 | D.4026 |
已知函数 的图象如图所示,则
的图象如图所示,则 满足的关系是( )
满足的关系是( )
A. | B.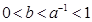 |
C. | D. |
设 ,则
,则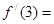 为( )
为( )
A. | B. | C. | D. |
已知函数 在区间
在区间 上是减函数,那么
上是减函数,那么 ( )
( )
A.有最小值 | B.有最大值 |
C.有最小值 | D.有最大值 |
 为定义在
为定义在 上的偶函数,对任意的
上的偶函数,对任意的

 为增函数,则下列各式成立的是 ( )
为增函数,则下列各式成立的是 ( )
A. | B. |
C. | D. |