题目内容
具有性质: 的函数,我们称为满足“倒负”变换的函数,下列函数:①
的函数,我们称为满足“倒负”变换的函数,下列函数:① ;②
;② ;③
;③ 中满足“倒负”变换的函数是( )
中满足“倒负”变换的函数是( )
| A.①② | B.①③ | C.②③ | D.只有① |
B
解析试题分析:对于①, ∴满足“倒负”变换;
∴满足“倒负”变换;
对于②,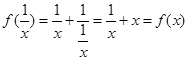 ≠-f(x);∴不满足“倒负”变换;
≠-f(x);∴不满足“倒负”变换;
对于③,当0<x<1时,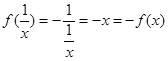 ,
,
当x=1时,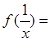 =0=-f(x),
=0=-f(x),
当x>1时,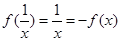
∴满足“倒负”变换.故应选B
考点:本题主要考查了新定义的理解和简单运用。
点评:解决该试新定义 型题,这类题的特点是依据定义来进行运算或判断,故审题中认真了解定义是做题的关键

练习册系列答案
相关题目
已知函数 ,函数
,函数 ,下列关于这两个函数的叙述正确的是( )
,下列关于这两个函数的叙述正确的是( )
A. 是奇函数, 是奇函数, 是奇函数 是奇函数 | B. 是奇函数, 是奇函数, 是偶函数 是偶函数 |
C. 是偶函数, 是偶函数, 是奇函数 是奇函数 | D. 是偶函数, 是偶函数, 是偶函数 是偶函数 |
函数 的单调递减区间是 ( )
的单调递减区间是 ( )
A. | B. | C. | D. |
设函数 的图像的交点为
的图像的交点为 ,则x0所在的区间是
,则x0所在的区间是
A. | B. | C. | D. |
函数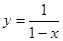 的图像与函数
的图像与函数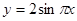 (
(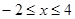 )的图像所有交点的横坐标之和等于 ( )
)的图像所有交点的横坐标之和等于 ( )
| A.2 | B.4 | C.6 | D.8 |
函数 对任意的
对任意的 恒有
恒有 且
且 ,则
,则 ( )
( )
A. | B. | C. | D. |
函数 的定义域是( ).
的定义域是( ).
A. | B. | C. | D. |
已知函数 在区间
在区间 上是减函数,那么
上是减函数,那么 ( )
( )
A.有最小值 | B.有最大值 |
C.有最小值 | D.有最大值 |
 与
与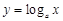 的图象可能是( )
的图象可能是( )