题目内容

| A.R | B.[-9,+ ) ) | C.[-8,1] | D.[-9,1] |
C
解析试题分析:由于当0 x
x 3,则函数开口向下,对称轴为x=1,那么在定义域先增厚减,那么可知函数的最小值为x=3时取得为-3,x=1取得最大值为1,;当-2
3,则函数开口向下,对称轴为x=1,那么在定义域先增厚减,那么可知函数的最小值为x=3时取得为-3,x=1取得最大值为1,;当-2 x
x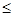 0时,则二次函数开口向上,对称轴为x=-3,那么可知在定义域内地增,那么可知函数的最小值为x=-2时取得为-8,最大值在x=0时取得为0.综上可知分段函数的值域是各段的并集可知为[-8,1],选C.
0时,则二次函数开口向上,对称轴为x=-3,那么可知在定义域内地增,那么可知函数的最小值为x=-2时取得为-8,最大值在x=0时取得为0.综上可知分段函数的值域是各段的并集可知为[-8,1],选C.
考点:本题主要考查了分段函数的 值域的求解。
点评:解决该试题的关键是对于二次函数的性质的熟练运用,掌握对称轴和定义域的关系,得到最值问题的求解。

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
已知函数 的图象如图所示,则
的图象如图所示,则 满足的关系是( )
满足的关系是( )
A. | B.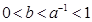 |
C. | D. |
已知函数 在区间
在区间 上是减函数,那么
上是减函数,那么 ( )
( )
A.有最小值 | B.有最大值 |
C.有最小值 | D.有最大值 |
若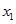 满足2x+
满足2x+ ="5,"
="5,"  满足2x+2
满足2x+2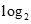 (x-1)="5,"
(x-1)="5," 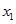 +
+ =
=
A. | B.3 | C. | D.4 |
已知函数 ,则
,则 是( )
是( )
| A.奇函数 | B.偶函数 |
| C.既是奇函数又是偶函数 | D.非奇函数非偶函数 |
若 为奇函数,在
为奇函数,在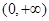 上单调递增,且
上单调递增,且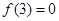 ,则
,则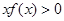 的解集为
的解集为
A.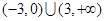 | B.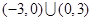 |
C.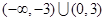 | D.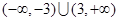 |
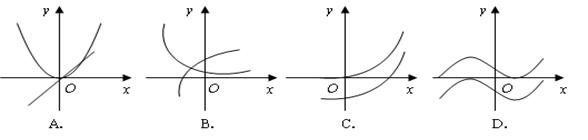
 与
与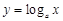 的图象可能是( )
的图象可能是( )
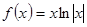 的大致图象是
的大致图象是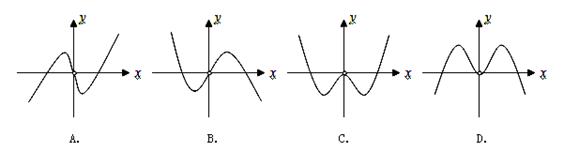
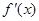 是函数
是函数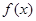 的导函数,将
的导函数,将 和
和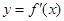 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )