题目内容
函数y=
的值域是( )
| -x2+2x+8 |
| A.(-∞,3] | B.[0,3] | C.[0,9] | D.[0,+∞) |
由-x2+2x+8≥0,即x2-2x-8≤0.
解得-2≤x≤4.
此时-x2+2x+8=-(x-1)2+9,
设t=-x2+2x+8,
则0≤t≤9,
即0≤
≤3,
∴函数y=
的值域是[0,3].
故选:B.
解得-2≤x≤4.
此时-x2+2x+8=-(x-1)2+9,
设t=-x2+2x+8,
则0≤t≤9,
即0≤
| t |
∴函数y=
| -x2+2x+8 |
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
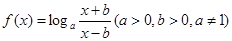 .
.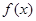 的定义域;
的定义域;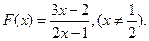

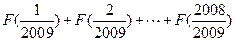 的值;
的值;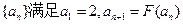 ,求数列
,求数列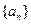 的通项公式;
的通项公式;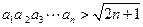 .
.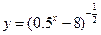 的定义域是 .
的定义域是 .