题目内容
(本题满分14分)
已知函数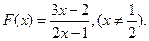

(1)求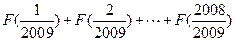 的值;
的值;
(2)已知数列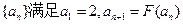 ,求数列
,求数列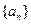 的通项公式;
的通项公式;
(3)求证: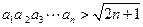 .
.
已知函数
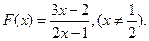

(1)求
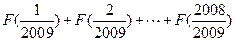 的值;
的值;(2)已知数列
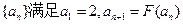 ,求数列
,求数列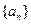 的通项公式;
的通项公式;(3)求证:
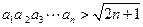 .
.(1)S=3012 (2)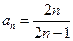
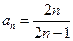
(1)因为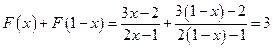 .…2分
.…2分
所以设S=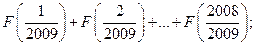 …………(1)
…………(1)
S=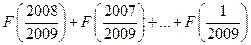 . ………(2)
. ………(2)
(1)+(2)得:
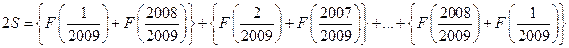 =
=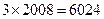 ,所以S="3012." …………………………………5分
,所以S="3012." …………………………………5分
(2)由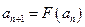 两边同减去1,得
两边同减去1,得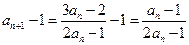 . ………………7分
. ………………7分
所以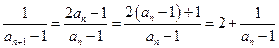 ,
,
所以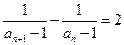 ,
,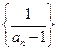 是以2为公差以
是以2为公差以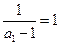 为首项的等差数列,
为首项的等差数列,
所以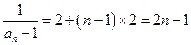
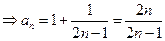 . …………10分
. …………10分
(3)因为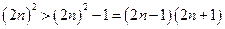
所以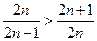
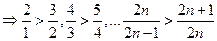 . ……………12分
. ……………12分
所以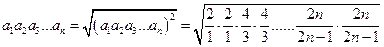
>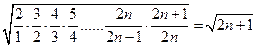 .…14分
.…14分
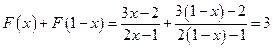 .…2分
.…2分所以设S=
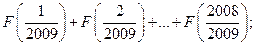 …………(1)
…………(1)S=
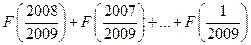 . ………(2)
. ………(2)(1)+(2)得:
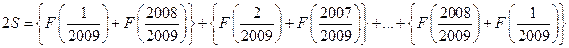 =
=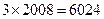 ,所以S="3012." …………………………………5分
,所以S="3012." …………………………………5分(2)由
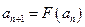 两边同减去1,得
两边同减去1,得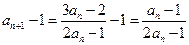 . ………………7分
. ………………7分所以
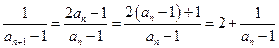 ,
,所以
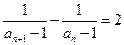 ,
,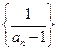 是以2为公差以
是以2为公差以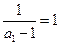 为首项的等差数列,
为首项的等差数列,所以
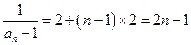
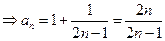 . …………10分
. …………10分(3)因为
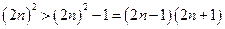
所以
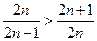
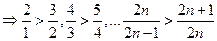 . ……………12分
. ……………12分所以
>
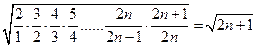 .…14分
.…14分
练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
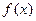 是抛物线,并且当点
是抛物线,并且当点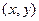 在抛物线图象上时,点
在抛物线图象上时,点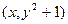 在函数
在函数 的图象上,求
的图象上,求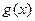 的解析式.
的解析式.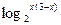 的定义域是( )
的定义域是( )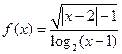 的定义域为 .
的定义域为 .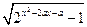 的定义域为R,
的定义域为R,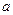 的取值范围为_______.
的取值范围为_______.