��Ŀ����
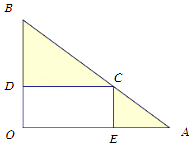
����Ŀ��ijѧУ�ü��������������ȡ��30��ͬѧ������ÿ��ƽ�������Ķ�ʱ�䣨��λ��Сʱ�����е��飬��Ҷͼ��ͼ��
�����¾������Ķ�ʱ�䲻����30Сʱ��ѧ����Ϊ�������ԡ�.
��1����Ƶ����Ϊ���ʣ����Ƹ�У900��ѧ���С������ԡ��ж����ˣ�
��2�����ѳ�ȡ��7���������ԡ��������ȡ�С�Ů�������ԡ���1�ˣ��μӶ����������.
��i�����ж����ֲ�ͬ�ij�ȡ������
��ii�����ȡ���С�Ů��λ�������ԡ��¾�����ʱ��������2Сʱ�ĸ���.
���𰸡�����210����������12�������� ![]() ��
��
����������������������ʿ���������������������������������������ɾ�Ҷͼ��֪���¾������Ķ�ʱ�䲻����30Сʱ��ѧ������Ϊ7�ˣ���ռ����Ϊ![]() ����˸�У900���еġ������ԡ�������Ϊ
����˸�У900���еġ������ԡ�������Ϊ![]() �ˣ������������ʿ���ŵ���ͻ����¼��ռ䣬���ȡ���С������ԡ�Ϊ
�ˣ������������ʿ���ŵ���ͻ����¼��ռ䣬���ȡ���С������ԡ�Ϊ![]() ��
�� ![]() ��
�� ![]() ����ȡ��Ů�������ԡ�Ϊ
����ȡ��Ů�������ԡ�Ϊ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() (�����½DZ��ʾ������ƽ�������Ķ�ʱ��)�����ǿ����г������¼��ռ䣻���������������֪�����������Ļ����¼�Ϊ
(�����½DZ��ʾ������ƽ�������Ķ�ʱ��)�����ǿ����г������¼��ռ䣻���������������֪�����������Ļ����¼�Ϊ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() �����ǿ����������.
�����ǿ����������.
����������������У900��ѧ���С������ԡ���![]() �ˣ���
�ˣ���![]() �����
�����![]() .
.
���Ը�У900��ѧ���С������ԡ�Լ��210��.
�����������ȡ���С������ԡ�Ϊ![]() ��
�� ![]() ��
�� ![]() ����ȡ��Ů�������ԡ�Ϊ
����ȡ��Ů�������ԡ�Ϊ
![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() (�����½DZ��ʾ������ƽ�������Ķ�ʱ��)��
(�����½DZ��ʾ������ƽ�������Ķ�ʱ��)��
���7���������ԡ��������ȡ�С�Ů�����Ը�1�˵����л����¼�Ϊ��
![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
���Թ���12�ֲ�ͬ�ij�ȡ������
��������A��ʾ�¼�����ȡ���С�Ů��λ�������¾�����ʱ��������2Сʱ����
���¼�A����![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]()
6�������¼���
�����������![]() ��
��

 Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�����Ŀ����Ʊ�г���ǰ������Դ��1602��������ڰ�ķ˹�غӴ����Ͻ��к�����ӡ�ȹ�˾��Ʊ��������������Ĺ�Ʊ�г����������������2017��2��26�ţ��й�֤�����ϯ��ʿ��̸�˶Թ��еļ��㽨�飬�����������������ģ��������ʦ������ʦ��Ҫ�����������ʽ����Ͷ�����ƣ���������Ͷ�ʷ�������һ���Ͷ��ӯ����������£�
��1��Ͷ�ʹ��У�
Ͷ�ʽ�� | ���� | ���ⲻ | ���� |
���� |
|
|
|
��2���������
Ͷ�ʽ�� | ���� | ���ⲻ | ���� |
���� |
|
|
|
����![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
������֪��������𡱿���ĸ��ʱȡ�Ͷ�ʹ��С�����ĸ���С����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
������֪��ʦ������ʦ�����˶�ѡ���ˡ��������������Ͷ�ʣ���������Ͷ�ʽ�����ֵĿ�������ͬ����һ�������������������һ�˻����ĸ��ʣ�