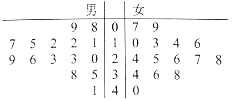
��Ŀ����
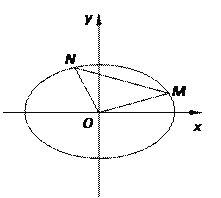
����Ŀ��ij����һ��ֱ�������εؿ飬�ּƻ����������һ����κ�����������������ͼ�����������������ֳ���ʩ�Ľ��裬������BCD����������ֲ���ֹ��ͻ��ܣ�������CAE����������ֲ���ֹ��ͻ��ܣ���֪OA=4ǧ�ף�OB=3ǧ�ף���AOB=90�㣬���ֻ���ÿƽ��ǧ�����1��Ԫ�����ֻ���ÿƽ��ǧ�����4��Ԫ����OE=xǧ�ף��Խ�����ֲ���ܵ������Ϊy����λ����Ԫ������x�ĺ�����ϵʽ����xΪ��ֵʱ����ֲ���ܵ��������С�����������ۣ� 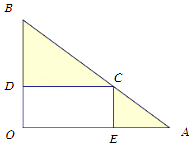
���𰸡��⣺�����⣬CD=OE=x���ɡ�BCD�ס�BAO֪BD= ![]() x������S��BCD=
x������S��BCD= ![]() x2 ��
x2 ��
ͬ����S��CAE= ![]() ��x��4��2
��x��4��2
���ԣ�y= ![]() [x2+��x��4��2��4]=
[x2+��x��4��2��4]= ![]() ��5x2��32x+64��������0��x��4��
��5x2��32x+64��������0��x��4��
y= ![]() [5��x��
[5��x�� ![]() ��2+
��2+ ![]() ]
]
��Ϊ0����4����14��
����x= ![]() ʱ��y����СֵΪ4.8��Ԫ��
ʱ��y����СֵΪ4.8��Ԫ��
��xΪ ![]() ʱ����ֲ���ܵ��������С���������СֵΪ4.8��Ԫ
ʱ����ֲ���ܵ��������С���������СֵΪ4.8��Ԫ
�����������������BCD��������CAE�����������ɵú�������ʽ�������䷽�����ɵú�������ֵ��

��ϰ��ϵ�д�
�����Ŀ