Question

3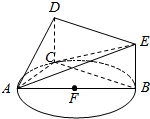．如图，△ABC内接于圆O，AB是圆的直径，四边形DCBE为平行四边形，DC⊥平面ABC，AB=2，BC=$\sqrt{3}$，BE=1．
（1）求三棱锥C-ABE的体积；
（2）已知M是线段CD的中点，求证：MO∥平面ADE．

Answer 1

分析 （1）利用等积法，求出三棱锥C-ABE的体积为V_{三棱锥C-ABE}=V_{三棱锥E-ABC}；
（2）取AE的中点N，连接DN、ON，证明四边形OMDN是平行四边形，得出OM∥DN，从而证明OM∥平面ADE．

解答 解：（1）三棱锥C-ABE的体积为
V_{三棱锥C-ABE}=V_{三棱锥E-ABC}
=$\frac{1}{3}$×S_△ABC•BE
=$\frac{1}{3}$×$\frac{1}{2}$•AC•BC•BE
=$\frac{1}{3}$×$\frac{1}{2}$×$\sqrt{{2}^{2}{-（\sqrt{3}）}^{2}}$×$\sqrt{3}$×1
=$\frac{\sqrt{3}}{6}$；
（2）证明：如图所示，

取AE的中点N，连接DN、ON，
则ON∥BE，ON=$\frac{1}{2}$BE=$\frac{1}{2}$，
又DM∥BE，DM=$\frac{1}{2}$CD=$\frac{1}{2}$，
∴ON∥DM，且ON=DM，
∴四边形OMDN是平行四边形，
OM∥DN，
又OM?平面ADE，DN?平面ADE，
∴OM∥平面ADE．

点评 本题考查了空间几何体的体积的计算问题，也考查了线面平行的判断问题，是基础题目．