题目内容
12.求Sn=1×2+3×4+5×8+…+(2n-1)2n.分析 利用错位相减法进行求解即可.
解答 解:∵Sn=1×2+3×4+5×8+…+(2n-1)2n.①
∴2Sn=1×4+3×8+5×16+…+(2n-1)2n+1.②,
①-②得-Sn=1×2+2×4+2×8+…+2•2n-(2n-1)2n+1=2+2(4+8+…+2n)-(2n-1)2n+1
=2+$2×\frac{4(1-{2}^{n-1})}{1-2}$)-(2n-1)2n+1
=2+8(2n-1-1)-(2n-1)2n+1
=2+2•2n+1-8-(2n-1)2n+1
=(3-2n)2n+1-6,
即Sn=(2n-3)2n+1+6.
点评 本题主要考查数列求和的计算,利用错位相减法是解决本题的关键.

练习册系列答案
相关题目
2.函数f(x)=ax2-$\sqrt{2}$(a>0),且f(f($\sqrt{2}$))=-$\sqrt{2}$,则a=( )
| A. | 1 | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
20.将函数f(x)=2sin(3x+$\frac{π}{4}$)的图象向左平移$\frac{π}{3}$个单位后得到函数y=g(x)的图象,则函数y=f(x)与函数y=g(x)的图象关于( )
| A. | x轴对称 | B. | 原点对称 | C. | y轴对称 | D. | 直线x=$\frac{π}{2}$对称 |
7.函数y=ln(x+1)与y=$\frac{a}{x}$的图象的一个交点的横坐标所在区间为(1,2),则实数a的取值范围是( )
| A. | (-∞,2ln3) | B. | (ln2,2ln3) | C. | (ln2,+∞) | D. | (-∞,2ln3)∪(ln2,+∞) |
2.函数y=$\frac{-2x-1}{2{x}^{2}-2x+3}$的极大值等于( )
| A. | $\frac{1}{5}$ | B. | -1 | C. | 1 | D. | -2 |
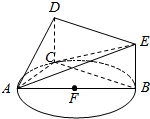 如图,△ABC内接于圆O,AB是圆的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,BC=$\sqrt{3}$,BE=1.
如图,△ABC内接于圆O,AB是圆的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,BC=$\sqrt{3}$,BE=1.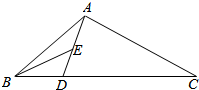 如图,在△ABC中,AB=AC=1,cos∠BAC=$\frac{1}{3}$,D是BC上一点,且DC=2BD,E是AD的中点,则BE的长为$\frac{\sqrt{129}}{18}$.
如图,在△ABC中,AB=AC=1,cos∠BAC=$\frac{1}{3}$,D是BC上一点,且DC=2BD,E是AD的中点,则BE的长为$\frac{\sqrt{129}}{18}$.