题目内容
13.已知函数f(x)=ln(1+x)-$\frac{ax}{x+2}$.(Ⅰ)当a=0时,求曲线y=f(x)在原点处的切线方程;
(Ⅱ)当a>0时,讨论函数f(x)在区间(0,+∞)上的单调性.
分析 (Ⅰ)求出导数,求得切线的斜率和切点,由点斜式方程,可得切线方程;
(Ⅱ)求出导数,对a讨论,当0<a≤2时,当a>2时,由导数大于0,可得增区间,由导数小于0,可得减区间.
解答 解:f(x)的导数$f'(x)=\frac{1}{1+x}-\frac{2a}{{{{(x+2)}^2}}}$=$\frac{{{x^2}+(4-2a)x+(4-2a)}}{{(x+1){{(x+2)}^2}}}$.
(Ⅰ)当a=0时,f(0)=0,切线的斜率k=f'(0)=1,
所以切线方程为y=x,即x-y=0.
(Ⅱ)当a>0时,因为x>0,
所以只要考查g(x)=x2+(4-2a)x+(4-2a)的符号.
由△=(4-2a)2-4(4-2a)≤0,得0<a≤2,
当0<a≤2时,g(x)>0,从而f'(x)>0,
f(x)在区间(0,+∞)上单调递增;
当a>2时,由g(x)=0解得$x=a-2+\sqrt{{a^2}-2a}$.
当0<x<a-2+$\sqrt{{a}^{2}-2a}$时,f′(x)<0,f(x)单调递减;
当x>a-2+$\sqrt{{a}^{2}-2a}$时,f′(x)>0,f(x)单调递增.
则函数f(x)在区间$(0,a-2+\sqrt{{a^2}-2a})$单调递减,
在区间$(a-2+\sqrt{{a^2}-2a},+∞)$上单调递增.
点评 本题考查导数的运用:求切线方程和单调区间,考查运算能力,运用分类讨论的思想方法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.设函数f(x)=$\left\{{\begin{array}{l}{\sqrt{x},\;x≥0}\\{-{x^2},x<0}\end{array}}$若f(a)+f(-1)=2,则a=( )
| A. | 3 | B. | 9 | C. | $\sqrt{3}$ | D. | -9 |
18.已知数列{an}的前n项和Sn=k-kan(a,k都是不为0的常数)是数列{an}为等比数列的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
2.函数y=$\frac{-2x-1}{2{x}^{2}-2x+3}$的极大值等于( )
| A. | $\frac{1}{5}$ | B. | -1 | C. | 1 | D. | -2 |
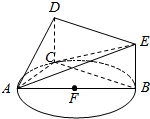 如图,△ABC内接于圆O,AB是圆的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,BC=$\sqrt{3}$,BE=1.
如图,△ABC内接于圆O,AB是圆的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,BC=$\sqrt{3}$,BE=1.