题目内容
18.已知函数f(x)=|x-a|-$\frac{8}{x}$,x∈[2,4].(1)当a=3时,求f(x)的单调区间;
(2)当a>0,求f(x)的最大值h(a).
分析 (1)去绝对值,讨论当3≤x≤4时,当2≤x<3时,运用函数的导数,可得单调性,进而得到单调区间;
(2)讨论a的范围,当a>4时,当a<2时,当2≤x≤a≤1+2$\sqrt{2}$时,当1+2$\sqrt{2}$<a≤4时,去掉绝对值,由喊话说的单调性可得最大值.
解答 解:(1)当a=3时,f(x)=|x-3|-$\frac{8}{x}$,x∈[2,4],
当3≤x≤4时,f(x)=x-$\frac{8}{x}$-3的导数为f′(x)=1+$\frac{8}{{x}^{2}}$>0,f(x)递增;
当2≤x<3时,f(x)=3-x-$\frac{8}{x}$的导数为f′(x)=-1+$\frac{8}{{x}^{2}}$,
当2$≤x<2\sqrt{2}$时,f′(x)>0,f(x)递增;
当2$\sqrt{2}$<x<3时,f′(x)<0,f(x)递减.
即有f(x)的增区间为(2,2$\sqrt{2}$),(3,4),减区间为(2$\sqrt{2}$,3);
(2)当a>4时,f(x)=a-x-$\frac{8}{x}$在(2,2$\sqrt{2}$)递增,在(2$\sqrt{2}$,4)递减,
即有最大值为f(2$\sqrt{2}$)=a-4$\sqrt{2}$;
当a<2时,f(x)=x-$\frac{8}{x}$-a在[2,4]递增,即有最大值为f(4)=2-a;
当2≤a≤4时,f(x)=$\left\{\begin{array}{l}{x-\frac{8}{x}-a,x≥a}\\{a-x-\frac{8}{x},x<a}\end{array}\right.$,
当2≤x≤a≤1+2$\sqrt{2}$时,f(x)递增,
即有最大值为f(4)=4-2-a=2-a;
当1+2$\sqrt{2}$<a≤4时,2-a<a-4$\sqrt{2}$,则最大值为a-4$\sqrt{2}$;
综上可得,当a>4时,f(x)的最大值为a-4$\sqrt{2}$;
当a<2时,f(x)的最大值为2-a;
当2≤a≤1+2$\sqrt{2}$时,f(x)的最大值为2-a;
当1+2$\sqrt{2}$<a≤4时,f(x)的最大值为a-4$\sqrt{2}$.
点评 本题考查含绝对值函数的单调区间和最值的求法,注意运用分类讨论的思想方法,考查运算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | (-∞,2ln3) | B. | (ln2,2ln3) | C. | (ln2,+∞) | D. | (-∞,2ln3)∪(ln2,+∞) |
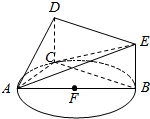 如图,△ABC内接于圆O,AB是圆的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,BC=$\sqrt{3}$,BE=1.
如图,△ABC内接于圆O,AB是圆的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,BC=$\sqrt{3}$,BE=1.