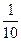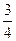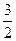题目内容
(本小题满分14分)函数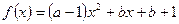 ,其中
,其中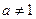 ,若存在实数
,若存在实数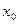 ,使得
,使得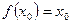 成立,则称
成立,则称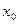 为
为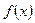 的不动点.
的不动点.
(1)当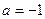 ,
,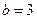 时,求
时,求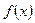 的不动点;
的不动点;
(2)若对于任何实数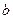 ,函数
,函数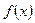 恒有两个相异的不动点,求实数
恒有两个相异的不动点,求实数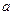 的取值范围;
的取值范围;
(3)在(2)的条件下,若函数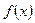 的图像上
的图像上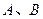 两点的横坐标是函数
两点的横坐标是函数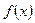 的不动点,且直线
的不动点,且直线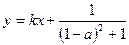 是线段
是线段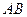 的垂直平分线,求实数
的垂直平分线,求实数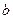 的取值范围.
的取值范围.
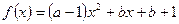 ,其中
,其中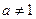 ,若存在实数
,若存在实数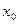 ,使得
,使得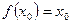 成立,则称
成立,则称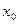 为
为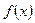 的不动点.
的不动点.(1)当
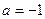 ,
,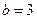 时,求
时,求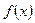 的不动点;
的不动点;(2)若对于任何实数
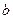 ,函数
,函数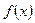 恒有两个相异的不动点,求实数
恒有两个相异的不动点,求实数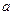 的取值范围;
的取值范围;(3)在(2)的条件下,若函数
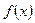 的图像上
的图像上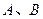 两点的横坐标是函数
两点的横坐标是函数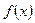 的不动点,且直线
的不动点,且直线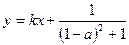 是线段
是线段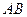 的垂直平分线,求实数
的垂直平分线,求实数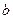 的取值范围.
的取值范围.(1)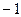 ,2
,2
(2)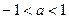
(3)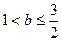
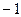 ,2
,2(2)
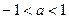
(3)
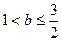
(1)当
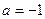 ,
,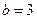 时,
时,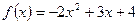 ,设
,设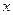 为不动点,则
为不动点,则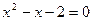 ,
,所以
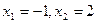 ,即
,即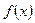 的不动点是
的不动点是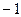 ,2。…………………………………(4分)
,2。…………………………………(4分)(2)由
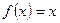 得,
得,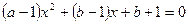 ,
,由已知此方程有相异的实根,则
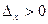 恒成立,即
恒成立,即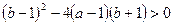 ,化简得
,化简得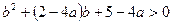 ………………………………(6分)
………………………………(6分)对任意的实数
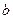 恒成立,则
恒成立,则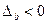 ,即
,即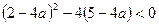 ,解得
,解得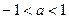 。…(8分)
。…(8分)(3)设
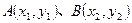 ,则
,则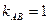 ,所以
,所以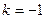 。
。记
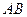 中点
中点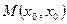 ,由(2)知
,由(2)知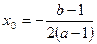 ,因为点
,因为点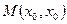 在直线
在直线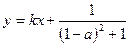 上,所以
上,所以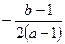 =
=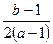
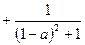 ,化简得
,化简得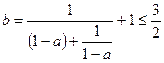 (当
(当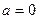 时,等号成立)………………………………(12分)
时,等号成立)………………………………(12分)又
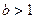 ,所以
,所以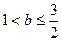 。…………………………………………………………(14分)
。…………………………………………………………(14分)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
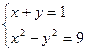 的解集是( )
的解集是( )
 B
B C
C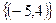 D
D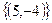
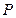 (元)与时间
(元)与时间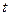 天的函数关系是
天的函数关系是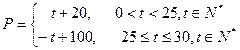 该商品的日销售量
该商品的日销售量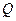 (件)与时间
(件)与时间 (1),求这种商品的日销售额
(1),求这种商品的日销售额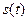 的解析式,(2)求
的解析式,(2)求
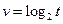
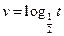
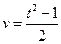
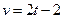
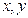 ,定义运算
,定义运算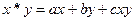 ,其中
,其中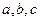 为常数,等号右边的运算是通常意义的加、乘运算.现已知
为常数,等号右边的运算是通常意义的加、乘运算.现已知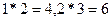 ,且有一个非零实数
,且有一个非零实数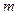 ,使得对任意实数
,使得对任意实数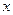 ,都有
,都有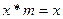 ,则
,则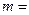 ( )
( )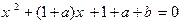 的两根为
的两根为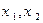 ,并且
,并且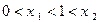 ,则
,则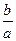 的取值范围是( )
的取值范围是( )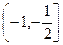
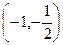

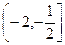
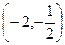
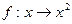 是集合
是集合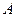 到集合
到集合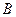 的映射,如果
的映射,如果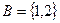 ,那么
,那么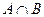 等于.
等于.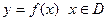 (定义域),若存在常数C,对于任意
(定义域),若存在常数C,对于任意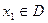 ,存在唯一的
,存在唯一的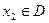 ,使得
,使得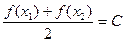 ,则称函数
,则称函数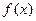 在D上的“均值”为C,已知
在D上的“均值”为C,已知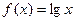 ,
,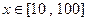 ,则函数
,则函数 上的均值为( )
上的均值为( )