题目内容
(本小题满分12分)
已知椭圆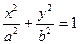 的右准线是
的右准线是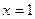 ,倾斜角为
,倾斜角为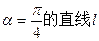 交椭圆于A、B两点,AB的中点为
交椭圆于A、B两点,AB的中点为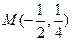
(I)求椭圆的方程;
(II)若P、Q是椭圆上满足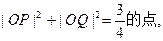 若直线OP、OQ的斜率分别为
若直线OP、OQ的斜率分别为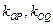 ,求证:
,求证: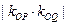 是定值。
是定值。
已知椭圆
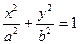 的右准线是
的右准线是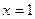 ,倾斜角为
,倾斜角为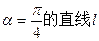 交椭圆于A、B两点,AB的中点为
交椭圆于A、B两点,AB的中点为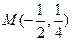
(I)求椭圆的方程;
(II)若P、Q是椭圆上满足
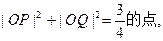 若直线OP、OQ的斜率分别为
若直线OP、OQ的斜率分别为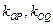 ,求证:
,求证: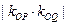 是定值。
是定值。(I)椭圆方程为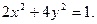
(II)证明略,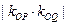
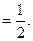
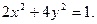
(II)证明略,
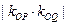
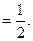
解:(I)由于直线AB的倾斜角为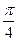 且过点
且过点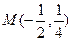 ,
,
所以直线的方程为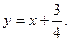
代入椭圆方程,整理得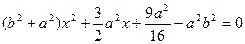 ,
,
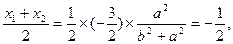
即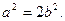
又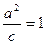 ,联立
,联立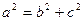 ,
,
求得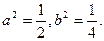
所以椭圆方程为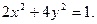 …………6分
…………6分
(II)设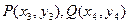 都在椭圆
都在椭圆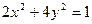 上,
上,
由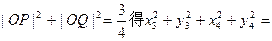
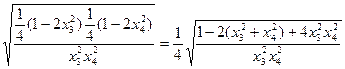
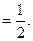 …………12分
…………12分
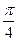 且过点
且过点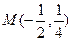 ,
,所以直线的方程为
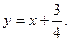
代入椭圆方程,整理得
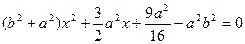 ,
,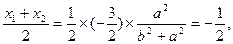
即
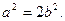
又
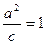 ,联立
,联立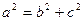 ,
,求得
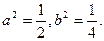
所以椭圆方程为
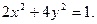 …………6分
…………6分(II)设
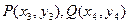 都在椭圆
都在椭圆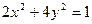 上,
上,由
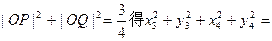
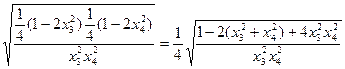
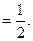 …………12分
…………12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
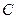 与椭圆
与椭圆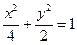 有相同的焦点,直线
有相同的焦点,直线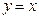 是双曲线
是双曲线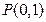 的直线
的直线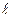 与双曲线
与双曲线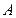 、
、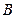 两点,若
两点,若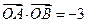 ,求直线
,求直线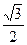 ,与直线x+y-1=0相交于两点M、N,且OM⊥ON.求椭圆的方程。
,与直线x+y-1=0相交于两点M、N,且OM⊥ON.求椭圆的方程。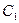 :
: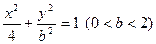 的离心率等于
的离心率等于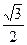 ,抛物线
,抛物线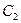 :
: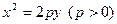 的焦点在椭圆的顶点上。
的焦点在椭圆的顶点上。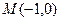 的直线
的直线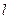 与抛物线
与抛物线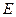 、
、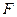 两点,又过
两点,又过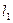 、
、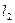 ,当
,当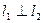 时,求直线
时,求直线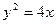 以F2为焦点,点P为抛物线和椭圆的一个交点,若PF2与x轴成45°,则e的值为 ▲ .
以F2为焦点,点P为抛物线和椭圆的一个交点,若PF2与x轴成45°,则e的值为 ▲ .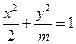 的离心率为
的离心率为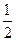 ,则m=" " ( )
,则m=" " ( )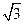 B
B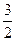 C
C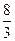 D
D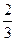
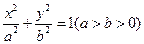 的离心率为e,焦点为F1、F2,抛物线C以F1为顶点,F2为焦点.设P为两条曲线的一个交点,若
的离心率为e,焦点为F1、F2,抛物线C以F1为顶点,F2为焦点.设P为两条曲线的一个交点,若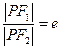 ,则e的值为( )
,则e的值为( )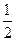
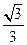
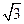

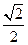
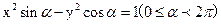 的焦点在y轴上,
的焦点在y轴上,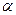 的取值范围是( )
的取值范围是( )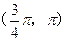

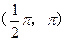
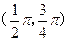
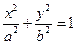 的左焦点
的左焦点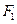 ,右顶点A,上顶点B,且
,右顶点A,上顶点B,且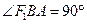 ,则椭圆的离心率是
,则椭圆的离心率是


