题目内容
如图,四棱锥S—ABCD的底面为正方形,SD 底面ABCD,则下列结论中正确的是 (把正确的答案都填上)
底面ABCD,则下列结论中正确的是 (把正确的答案都填上)
(1)AC⊥SB
(2)AB∥平面SCD
(3)SA与平面SBD所成的角等于SC与平面SBD所成的角
(4)AB与SC所成的角等于DC与SA所成的角
(1),(2),(3)
解析试题分析:∵SD⊥底面ABCD,底面ABCD为正方形,
∴连接BD,则BD⊥AC,根据三垂线定理,可得AC⊥SB,故(1)正确;
∵AB∥CD,AB?平面SCD,CD?平面SCD,
∴AB∥平面SCD,故(2)正确;
∵SD⊥底面ABCD,
∠ASO是SA与平面SBD所成的角,∠DSO是SC与平面SBD所成的,
而△SAO≌△CSO,
∴∠ASO=∠CSO,即SA与平面SBD所成的角等于SC与平面SBD所成的角,故(3)正确;
∵AB∥CD,∴AB与SC所成的角是∠SCD,DC与SA所成的角是∠SAB,
而这两个角显然不相等,故(4)不正确;
故选D.
考点:本题主要考查线面垂直的性质定理和线面平行的判定定理,以及直线与平面所成的角,异面直线所成的角问题。
点评:小综合题,本题是涉及立体几何平行关系、垂直关系的典型题目。较全面的考查了线线关系、线面关系等,该几何模型也十分典型。

练习册系列答案
相关题目
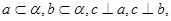 则
则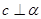 ;②。若
;②。若 则
则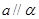 ;
;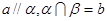 ,则
,则 ; ④。若
; ④。若 ,则
,则 边长为
边长为 ,角
,角 ,沿
,沿 将
将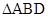 折起,使二面角
折起,使二面角 为
为 ,则折起后
,则折起后 、
、 之间的距离是 .
之间的距离是 .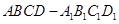 中,
中, ,
,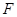 分别是棱
分别是棱 ,
, 的中点,则
的中点,则 与平面
与平面
 的底面是正方形,侧棱与底面边长均为2,则其侧视图的面积为_____.
的底面是正方形,侧棱与底面边长均为2,则其侧视图的面积为_____.

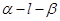 的大小是60°,线段
的大小是60°,线段 .
. ,
,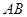 与
与 所成的角为30°.则
所成的角为30°.则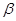 所成的角的正弦值是 .
所成的角的正弦值是 .
 的平面角是锐角
的平面角是锐角 ,平面
,平面 内有一点
内有一点 到
到 的距离为3,点
的距离为3,点 距离为4,那么
距离为4,那么 =
=