题目内容
对于函数 ,若
,若 都是某一三角形的三边长,则称
都是某一三角形的三边长,则称 为“可构造三角形函数”.以下说法正确的是( )
为“可构造三角形函数”.以下说法正确的是( )
A. 不是“可构造三角形函数”; 不是“可构造三角形函数”; |
| B.“可构造三角形函数”一定是单调函数; |
C. 是“可构造三角形函数”; 是“可构造三角形函数”; |
D.若定义在 上的函数 上的函数 的值域是 的值域是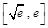 ( ( 为自然对数的底数),则 为自然对数的底数),则 一定是“可构造三角形函数”. 一定是“可构造三角形函数”. |
D.
解析试题分析:本题考查了对新定义“可构造三角形函数”的判定,要结合函数值域,三角形知识进行判别.A选项: ,则
,则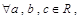 有
有 ,可构造三边边长为1的正三角形,∴A错.B选项:由“可构造三角形函数”定义可知,若
,可构造三边边长为1的正三角形,∴A错.B选项:由“可构造三角形函数”定义可知,若 为单调函数,不一定能满足三角形中“两边之和大于第三边,两边之差小于第三边”,∴B错.C 选项:
为单调函数,不一定能满足三角形中“两边之和大于第三边,两边之差小于第三边”,∴B错.C 选项: ,有
,有 ,若第三边
,若第三边 ,则不符合三角形函数.
,则不符合三角形函数. ,则第三边无法取到大于1的值,∴C错误.D选项:若
,则第三边无法取到大于1的值,∴C错误.D选项:若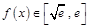 ,则
,则 一定能满足三角形中“任意两边之和大于第三边”,
一定能满足三角形中“任意两边之和大于第三边”,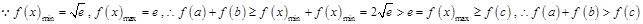 ,由定义可知
,由定义可知 一定是“可构造三角形函数”,∴选D.
一定是“可构造三角形函数”,∴选D.
考点:1.新定义的创新问题;2.函数的值域.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数 是定义在R上的偶函数, 且在区间
是定义在R上的偶函数, 且在区间 单调递增.若实数
单调递增.若实数 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D.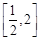 |
下列各组函数表示同一函数的是( )
A. | B. |
C. | D. |
下列函数中,与函数 相同的是( )
相同的是( )
A. | B.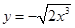 | C. | D. |
已知函数f(x)是定义在R上的奇函数,且当x∈(-∞,0]时,f(x)=e-x-ex2+a,则函数f(x)在x=1处的切线方程为( )
| A.x+y=0 | B.ex-y+1-e=0 |
| C.ex+y-1-e=0 | D.x-y=0 |
在某个物理实验中,测得变量x和变量y的几组数据,如下表:
| x | 0.50 | 0.99 | 2.01 | 3.98 |
| y | -0.99 | 0.01 | 0.98 | 2.00 |
(A)y=2x (B)y=x2-1
(C)y=2x-2 (D)y=log2x
设f(x)是连续的偶函数,且当x>0时是单调函数,则满足f(2x)=f(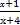 )的所有x之和为( )
)的所有x之和为( )
A.- | B.- | C.-8 | D.8 |