题目内容
已知函数f(x)是定义在R上的奇函数,且当x∈(-∞,0]时,f(x)=e-x-ex2+a,则函数f(x)在x=1处的切线方程为( )
| A.x+y=0 | B.ex-y+1-e=0 |
| C.ex+y-1-e=0 | D.x-y=0 |
B
解析

练习册系列答案
相关题目
函数 的定义域是( )
的定义域是( )
A. | B. | C. | D. |
设 是
是 上的奇函数,且
上的奇函数,且 时,
时, ,对任意
,对任意 ,不等式
,不等式 恒成立,则
恒成立,则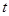 的取值范围( )
的取值范围( )
A. | B. | C. | D. |
若函数 的导函数在区间
的导函数在区间 上的图像关于直线
上的图像关于直线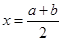 对称,则函数
对称,则函数 在区间
在区间 上的图象可能是( )
上的图象可能是( )
| A.①④ | B.②④ | C.②③ | D.③④ |
对于函数 ,若
,若 都是某一三角形的三边长,则称
都是某一三角形的三边长,则称 为“可构造三角形函数”.以下说法正确的是( )
为“可构造三角形函数”.以下说法正确的是( )
A. 不是“可构造三角形函数”; 不是“可构造三角形函数”; |
| B.“可构造三角形函数”一定是单调函数; |
C. 是“可构造三角形函数”; 是“可构造三角形函数”; |
D.若定义在 上的函数 上的函数 的值域是 的值域是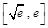 ( ( 为自然对数的底数),则 为自然对数的底数),则 一定是“可构造三角形函数”. 一定是“可构造三角形函数”. |
设f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1-x),则f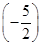 等于( )
等于( )
A.- | B.- | C. | D. |
函数f(x)= -
- 的定义域是( )
的定义域是( )
| A.{x|2≤x≤3} | B.{x|2≤x<3} |
| C.{x|0<x<3} | D.{x|x>3} |
定义在R上的函数f(x)满足f(x+y)=f(x)+f(y),当x<0时,f(x)>0,则函数f(x)在[a,b]上有( )
| A.最小值f(a) | B.最大值f(b) |
| C.最小值f(b) | D.最大值f( ) ) |

