题目内容
规定记号“?”表示一种运算,即a?b=a2+2ab-b2.设函数f(x)=x?2,且关于x的方程f(x)=lg|x+2|(x≠-2)恰有四个互不相等的实数根x1,x2,x3,x4,则x1+x2+x3+x4的值是( )
| A.-4 | B.4 | C.8 | D.-8 |
D
解析

练习册系列答案
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
对于函数 ,若
,若 都是某一三角形的三边长,则称
都是某一三角形的三边长,则称 为“可构造三角形函数”.以下说法正确的是( )
为“可构造三角形函数”.以下说法正确的是( )
A. 不是“可构造三角形函数”; 不是“可构造三角形函数”; |
| B.“可构造三角形函数”一定是单调函数; |
C. 是“可构造三角形函数”; 是“可构造三角形函数”; |
D.若定义在 上的函数 上的函数 的值域是 的值域是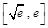 ( ( 为自然对数的底数),则 为自然对数的底数),则 一定是“可构造三角形函数”. 一定是“可构造三角形函数”. |
下列函数中,既是偶函数又在区间 上单调递增的函数是( )
上单调递增的函数是( )
A. | B. | C. | D. |
定义在R上的函数f(x)满足f(x+y)=f(x)+f(y),当x<0时,f(x)>0,则函数f(x)在[a,b]上有( )
| A.最小值f(a) | B.最大值f(b) |
| C.最小值f(b) | D.最大值f( ) ) |
下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是( )
A.y= | B.y=e-x | C.y=-x2+1 | D.y=lg |x| |
已知函数f(x)是定义域为R上的奇函数,且周期为2.若当x∈[0,1)时,f(x)=2x-1,则f( 的值是 ( ).
的值是 ( ).
A.- | B.-5 | C.- | D.-6 |
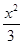 -cos 2x的图像大致是( )
-cos 2x的图像大致是( )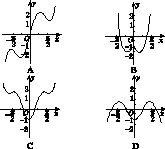

 的图象是( ).
的图象是( ).
