题目内容
【题目】探究函数![]() 的图象与性质.
的图象与性质.
(1)下表是y与x的几组对应值.
| … |
|
|
|
|
|
|
| … |
| … |
|
|
|
|
|
|
| … |
其中m的值为_______________;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并已画出了函数图象的一部分,请你画出该图象的另一部分;

(3)结合函数的图象,写出该函数的一条性质:_________;
(4)若关于x的方程![]() 有2个实数根,则t的取值范围是______.
有2个实数根,则t的取值范围是______.
【答案】(1)3;(2)图象见解析;(3)图象关于直线x=1轴对称.(答案不唯一);(4)t>1或t=0.
【解析】
(1)把x=3代入解析式计算即可得出m的值;
(2)画出图象即可;
(3)根据图象得出性质;
(4)观察图象即可得出结论.
解:(1)当x=3时,y=![]() =3,∴m=3;
=3,∴m=3;
(2)如图所示:
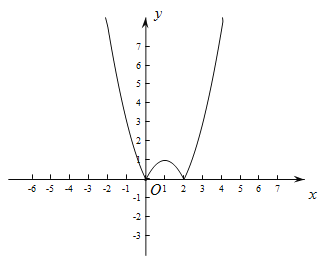
(3)图象关于直线x=1轴对称.(答案不唯一)
(4)观察图象可知:当t>1或t=0时,关于x的方程![]() 有2个实数根.
有2个实数根.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案【题目】若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数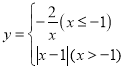 的图象与性质.列表:
的图象与性质.列表:
x | … |
|
|
|
|
|
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … |
|
| 1 |
| 2 |
| 1 |
| 0 |
| 1 |
| 2 | … |
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示.
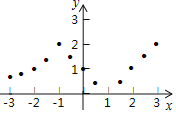
(1)如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象;
(2)研究函数并结合图象与表格,回答下列问题:
①点![]() ,
,![]() ,
,![]() ,
,![]() 在函数图象上,
在函数图象上,![]()
![]() ,
,![]()
![]() ;(填“>”,“=”或“<”)
;(填“>”,“=”或“<”)
②当函数值![]() 时,求自变量x的值;
时,求自变量x的值;
③在直线![]() 的右侧的函数图象上有两个不同的点
的右侧的函数图象上有两个不同的点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
④若直线![]() 与函数图象有三个不同的交点,求a的取值范围.
与函数图象有三个不同的交点,求a的取值范围.
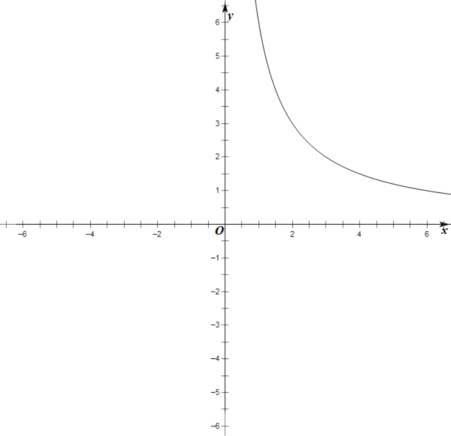
【题目】某班数学兴趣小组对函数![]() 的图象和性质将进行了探究,探究过程如下,请补充完整.
的图象和性质将进行了探究,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是除
的取值范围是除![]() 外的全体实数,
外的全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() _________;
_________;
(2)根据上表数据,在如图所示的平面直角坐标系中描点并画出了函数图象的一部分,请画出该函数图象的另一部分;
(3)观察函数图象,写出一条函数性质;
(4)进一步探究函数图象发现:
①函数图象与![]() 轴交点情况是________,所以对应方程
轴交点情况是________,所以对应方程![]() 的实数根的情况是________;
的实数根的情况是________;
②方程![]() 有_______个实数根;
有_______个实数根;
③关于![]() 的方程
的方程![]() 有
有![]() 个实数根,
个实数根,![]() 的取值范围是________.
的取值范围是________.
【题目】某市为了了解校园安全教育系列活动的成效,对全市高中生进行一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化,现随机抽取部分高中生的答卷,统计结果如下,对应的频率分布直方图如图所示.
等级 | 不合格 | 合格 | ||
得分 | [20,40) | [40,60) | [60,80) | [80,100) |
频数 | 12 |
| 48 | 24 |
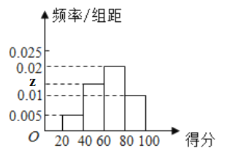
(1)求![]() 、
、![]() 的值;
的值;
(2)估计该市高中生测试成绩评定等级为“合格”的概率;
(3)在抽取的答卷中,用分层抽样的方法,从评定等级为“合格”和“不合格”的答卷中抽取5份,再从这5份答卷中任取2份,求恰有1份评定等级为“不合格”的概率
