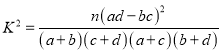题目内容
【题目】已知函数![]()
![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程.
处的切线方程.
(2)求函数![]() 的单调区间.
的单调区间.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:
(1)函数的定义域![]() ,当
,当![]() 时,计算可得:
时,计算可得:![]() ,
,![]() ,则切线方程为
,则切线方程为![]() .
.
(2)![]() ,考查二次函数
,考查二次函数![]() ,分类讨论:
,分类讨论:
①若![]() ,
,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
②若![]() ,
,![]() 为开口向上的二次函数,两个零点均在定义域
为开口向上的二次函数,两个零点均在定义域![]() 上.则:
上.则:
(i)若![]() ,函数
,函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(ii)若![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
(iii)若![]() ,函数
,函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
试题解析:
(1)函数的定义域![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,∴切线方程为
,∴切线方程为![]() .
.
(2)![]() ,
,
易知![]() ,令
,令![]() ,
,
①若![]() ,
,![]() ,∴
,∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
②若![]() ,
,![]() 为开口向上的二次函数,零点分别为0,
为开口向上的二次函数,零点分别为0,![]() ,其中
,其中![]() ,
,
即![]() 的两个零点均在定义域
的两个零点均在定义域![]() 上.
上.
(i)若![]() ,
,![]() ,所以函数
,所以函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(ii)若![]() ,
,![]() ,
,![]() 图象恒在
图象恒在![]() 轴上方,
轴上方,![]() 恒成立,∴
恒成立,∴![]() 在
在![]() 上单调递增.
上单调递增.
(iii)若![]() ,
,![]() ,∴函数
,∴函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.

【题目】探究函数![]() 的图象与性质.
的图象与性质.
(1)下表是y与x的几组对应值.
| … |
|
|
|
|
|
|
| … |
| … |
|
|
|
|
|
|
| … |
其中m的值为_______________;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并已画出了函数图象的一部分,请你画出该图象的另一部分;

(3)结合函数的图象,写出该函数的一条性质:_________;
(4)若关于x的方程![]() 有2个实数根,则t的取值范围是______.
有2个实数根,则t的取值范围是______.
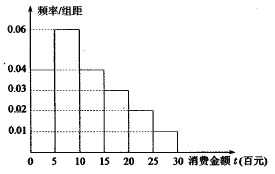
【题目】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的![]() 人(男、女各
人(男、女各![]() 人),记录了他们某一天的走路步数,并将数据整理如下:
人),记录了他们某一天的走路步数,并将数据整理如下:
步量 性别 | 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 | >10000 |
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
(1)已知某人一天的走路步数超过![]() 步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的
步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有
列联表,并据此判断能否有![]() 以上的把握认为“评定类型”与“性别”有关?
以上的把握认为“评定类型”与“性别”有关?
积极型 | 懈怠型 | 总计 | |
男 | |||
女 | |||
总计 |
附:![]() ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)若小王以这![]() 位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选
位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选![]() 人,其中每日走路不超过
人,其中每日走路不超过![]() 步的有
步的有![]() 人,超过
人,超过![]() 步的有
步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.